Trip Assignment

Lecture notes in Transportation Systems Engineering

August 23, 2011

Overview

The process of allocating given set of trip interchanges to the specified transportation system is usually referred to as trip assignment or traffic assignment. The fundamental aim of the traffic assignment process is to reproduce on the transportation system, the pattern of vehicular movements which would be observed when the travel demand represented by the trip matrix, or matrices, to be assigned is satisfied. The major aims of traffic assignment procedures are:

1. To estimate the volume of traffic on the links of the network and obtain aggregate network measures.
2. To estimate inter zonal travel cost.
3. To analyze the travel pattern of each origin to destination(O-D) pair.
4. To identify congested links and to collect traffic data useful for the design of future junctions.

Link cost function

As the flow increases towards the capacity of the stream, the average stream speed reduces from the free flow speed to the speed corresponding to the maximum flow. This can be seen in the graph shown below.

Figure 1: Two Link Problem with constant travel time function

That means traffic conditions worsen and congestion starts developing. The inter zonal flows are assigned to the minimum paths computed on the basis of free-flow link impedances (usually travel time). But if the link flows were at the levels dictated by the assignment, the link speeds would be lower and the link travel time would be higher than those corresponding to the free flow conditions. So the minimum path computed prior to the trip assignment will not be the minimum after the trips ae assigned. A number of iterative procedures are done to converge this difference. The relation between the link flow and link impedance is called the link cost function and is given by the equation as shown below:

$$t = t_0 {[1+{\alpha} {{(\frac{x}{k})}^{\beta}}]} % Link Travel Time Functin$$ (1)

where $t$ and $x$ is the travel time and flow, respectively on the link, $t_0$ is the free flow travel time, and k is the practical capacity. The parameters $\alpha$ and $\beta$ are specific the type of link and is to be calibrated from the field data. In the absense of any field data, following values could the assumed: $\alpha$ = 0.15, and $\beta$ = 4.0.

The types of traffic assignment models are all-or-nothing assignment (AON), incremental assignment, capacity restraint assignment, user equilibrium assignment (UE), stochastic user equilibrium assignment (SUE), system optimum assignment (SO), etc. The frequently used models all-or-nothing, user equilibrium, and system optimum will be discussed in detail here.

All-or-nothing assignment

In this method the trips from any origin zone to any destination zone are loaded onto a single, minimum cost, path between them. This model is unrealistic as only one path between every O-D pair is utilized even if there is another path with the same or nearly same travel cost. Also, traffic on links is assigned without consideration of whether or not there is adequate capacity or heavy congestion; travel time is a fixed input and does not vary depending on the congestion on a link. However, this model may be reasonable in sparse and uncongested networks where there are few alternative routes and they have a large difference in travel cost. This model may also be used to identify the desired path : the path which the drivers would like to travel in the absence of congestion. In fact, this model's most important practical application is that it acts as a building block for other types of assignment techniques.It has a limitation that it ignores the fact that link travel time is a function of link volume and when there is congestion or that multiple paths are used to carry traffic.

Example

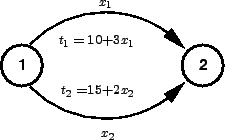
To demonstrate how this assignment works, an example network is considered. This network has two nodes having two paths as links. Let us suppose a case where travel time is not a function of flow as shown in other words it is constant as shown in the figure below.

Figure 2: Two Link Problem with constant travel time function

Solution

The travel time functions for both the links is given by:

$t_1 = 10$

$t_2 = 15$

and total flows from 1 to 2 is given by. $q_{12} = 12$

Since the shortest path is Link 1 all flows are assigned to it making $x_1$ =12 and $x_2$ = 0.

User equilibrium assignment (UE)

The user equilibrium assignment is based on Wardrop's first principle, which states that no driver can unilaterally reduce his/her travel costs by shifting to another route. User Equilibrium (UE) conditions can be written for a given O-D pair as:

$$f_k(c_k - u) = 0 :\forall k$$ (2)

$$c_k - u >= 0 :\forall k$$ (3)

where $f_k$ is the flow on path $k$, $c_k$ is the travel cost on path $k$, and $u$ is the minimum cost. Equation 3 can have two states.

1. If $c_k-u$ = 0, from equation 2 $f_k\ge$ 0. This means that all used paths will have same travel time.
2. If $c_k-u$ $\ge$ 0, then from equation 2 $f_k$ = 0.

This means that all unused paths will have travel time greater than the minimum cost path. where $f_k$ is the flow on path $k$, $c_k$ is the travel cost on path $k$, and $u$ is the minimum cost.

Assumptions in User Equilibrium Assignment

1. The user has perfect knowledge of the path cost.
2. Travel time on a given link is a function of the flow on that link only.
3. Travel time functions are positive and increasing.

The solution to the above equilibrium conditions given by the solution of an equivalent nonlinear mathematical optimization program,

$${\mathrm{Minimize   }}Z = \sum_{a}\int_0^{x_{a}}t_{a}(x_{a})dx,$$ (4)

$${\mathrm{subjected to   }}\sum_{k}f_k^{rs} = q_{rs}   : \forall r,s$$

$$x_a = \sum_r \sum_s \sum_k \delta_{a,k}^{rs}f_k^{rs}   : \forall a$$

$$f_k^{rs} \geq 0   : \forall  k,r,s$$

$$x_a \geq 0   : a \in A \nonumber$$

where $k$ is the path, $x_a$ equilibrium flows in link a, $t_a$ travel time on link a, $f_k^{rs}$ flow on path k connecting O-D pair r-s, $q_{rs}$ trip rate between r and sand $\delta_{a,k}^{rs}$ is a definitional constraint and is given by

$$\delta_{a,k}^{r,s}=\left\{ \begin{array}{cc} 1 & {\mathrm{if... ...ath k,}} \\ 0 & {\mathrm{otherwise}} \\ \end{array}\right.$$ (5)

The equations above are simply flow conservation equations and non negativity constraints, respectively. These constraints naturally hold the point that minimizes the objective function. These equations state user equilibrium principle.The path connecting O-D pair can be divided into two categories : those carrying the flow and those not carrying the flow on which the travel time is greater than (or equal to)the minimum O-D travel time. If the flow pattern satisfies these equations no motorist can better off by unilaterally changing routes. All other routes have either equal or heavy travel times. The user equilibrium criteria is thus met for every O-D pair. The UE problem is convex because the link travel time functions are monotonically increasing function, and the link travel time a particular link is independent of the flow and other links of the networks. To solve such convex problem Frank Wolfe algorithm is useful.

Example

Let us suppose a case where travel time is not a function of flow as shown in other words it is constant as shown in the figure below.

Figure 3: Two Link Problem with constant travel time function

Solution

Substituting the travel time in equation yield to

$$\begin{eqnarray*} \nonumber min Z(x)= \displaystyle\int^{x_1}_0 10+3x_1 dx_1 + ... ..._2 dx_2 = 10x_1 + \frac{3x_1^2}{2} + 15x_2 + \frac{2x_2^2}{2} \end{eqnarray*}$$

subject to

$$\begin{eqnarray*} \nonumber x_1 + x_2 = 12 \end{eqnarray*}$$

Substituting $x_2= 12-x_1$, in the above formulation will yield the unconstrained formulation as below :

$$min Z(x)= 10x_1 + \frac{3x_1^2}{2} + 15(12-x_1) + \frac{2(12-x_1)^2}{2}$$

Differentiate the above equation $x_1$ and equate to zero, and solving for $x_1$ and then $x_2$ leads to the solution $x_1$ = 5.8, $x_2$ = 6.2.

System Optimum Assignment (SO)

The system optimum assignment is based on Wardrop's second principle, which states that drivers cooperate with one another in order to minimize total system travel time. This assignment can be thought of as a model in which congestion is minimized when drivers are told which routes to use. Obviously, this is not a behaviorally realistic model, but it can be useful to transport planners and engineers, trying to manage the traffic to minimize travel costs and therefore achieve an optimum social equilibrium.

$${\mathrm Minimize  }Z = \sum_{a} x_{a}t_{a}(x_{a})$$ (6)

subject to

$$\sum_{k}f_k^{rs}=q_{rs} :\forall r,s$$ (7)

$$x_a = \sum_r \sum_s \sum_k \delta_{a,k}^{rs}f_k^{rs} :\forall a$$ (8)

$$f_k^{rs} \geq 0 : \forall  k,r,s$$ (9)

$$x_a \geq 0 : a \in A$$ (10)

$x_a$ equilibrium flows in link a, $t_a$ travel time on link a, $f_k^{rs}$ flow on path k connecting O-D pair r-s, $q_{rs}$ trip rate between r and s.

Example

To demonstrate how the assignment works, an example network is considered. This network has two nodes having two paths as links. Let us suppose a case where travel time is not a function of flow or in other words it is constant as shown in the figure below.

Figure 4: Two Link Problem with constant travel time function

Solution

Substituting the travel time in equation , we get the following:

$$min Z(x)= {x_1}*({10+3x_1}) + {x_2}*({15+2x_2})$$ (11)

$$= 10{x_1}+3{x_1}^2 + 15{x_2}+2{x_2}^2$$ (12)

Substituting $x_2= x_1-12$

$$min Z(x)= = 10{x_1}+3{x_1}^2 + 15{(12-x_1)}+2{(12-x_1)}^2$$ (13)

Differentiate the above equation to zero, and solving for $x_1$ and then $x_2$ leads to the solution $x_1$ = 5.3,$x_2$= 6.7 which gives Z(x) = 327.55

Other assignment methods

Let us discuss briefly some other assignments like incremental assignment, capacity restraint assignment, stochastic user equilibrium assignment and dynamic assignment.

Incremental assignment

Incremental assignment is a process in which fractions of traffic volumes are assigned in steps.In each step, a fixed proportion of total demand is assigned, based on all-or-nothing assignment. After each step, link travel times are recalculated based on link volumes. When there are many increments used, the flows may resemble an equilibrium assignment ; however, this method does not yield an equilibrium solution. Consequently, there will be inconsistencies between link volumes and travel times that can lead to errors in evaluation measures. Also, incremental assignment is influenced by the order in which volumes for O-D pairs are assigned, raising the possibility of additional bias in results.

Capacity restraint assignment

Capacity restraint assignment attempts to approximate an equilibrium solution by iterating between all-or-nothing traffic loadings and recalculating link travel times based on a congestion function that reflects link capacity. Unfortunately, this method does not converge and can flip-flop back and forth in loadings on some links.

Stochastic user equilibrium assignment

User equilibrium assignment procedures based on Wardrop's principle assume that all drivers perceive costs in an identical manner. A solution to assignment problem on this basis is an assignment such that no driver can reduce his journey cost by unilaterally changing route. Van Vilet considered as stochastic assignment models, all those models which explicitly allows non minimum cost routes to be selected. Virtually all such models assume that drivers perception of costs on any given route are not identical and that the trips between each O-D pair are divided among the routes with the most cheapest route attracting most trips. They have important advantage over other models because they load many routes between individual pairs of network nodes in a single pass through the tree building process,the assignments are more stable and less sensitive to slight variations in network definitions or link costs to be independent of flows and are thus most appropriate for use in uncongested traffic conditions such as in off peak periods or lightly trafficked rural areas.

Dynamic Assignment

Dynamic user equilibrium,expressed as an extension of Wardrop's user equilibrium principle, may be defined as the state of equilibrium which arises when no driver can reduce his disutility of travel by choosing a new route or departure time,where disutility includes, schedule delay in addition in to costs generally considered. Dynamic stochastic equilibrium may be similarly defined in terms of perceived utility of travel. The existence of such equilibrium in complex networks has not been proven theoretical and even if they exist the question of uniqueness remains open.

Summary

Traffic assignment is the last stage of traffic demand modeling. There are different types of traffic assignment models. All-or-nothing, User-equilibrium, and System-optimum assignment models are the commonly used models. All-or-nothing model is an unrealistic model since only one path between every O-D pair is utilised and they can give satisfactory results only when the network is least congested. User-equilibrium assignment is based on Wardrop's first principle and it's conditions are based on certain assumptions. Wardrop's second principle is utilized by System-optimum method and it tries to minimise the congestion by giving prior information to drivers regarding the respective routes to be chosen. Other assignment models are also briefly explained.

Problems

Calculate the system travel time and link flows by doing user equilibrium assignment for the network in the given figure 5. Verify that the flows are at user equilibrium.

Figure 5: Two link problem with constant travel time

Solution

Substituting the travel time in the respective equation yield to

$$\begin{eqnarray*} \nonumber \min Z(x)= \displaystyle\int^{x_1}_0 12+3x_1 dx_1 + ... ...2 dx_2 \\ = 12x_1 + \frac{3x_1^2}{2} + 10x_2 + \frac{5x_2^2}{2} \end{eqnarray*}$$

subject to

$$\begin{eqnarray*} \nonumber x_1 + x_2 = 12 \end{eqnarray*}$$

Substituting $x_2= 12-x_1$, in the above formulation will yield the unconstrained formulation as below :

$$\min Z(x)= 12x_1 + \frac{3x_1^2}{2} + 10(12-x_1) + \frac{5(12-x_1)^2}{2} \nonumber \min Z(x)=4x_1^2-58x_1+480$$

Differentiate the above equation $x_1$ and equating to zero,

$$\begin{eqnarray*} \frac{d{z(x)}}{dx}=0 -58+8x_1=0 or x_1=7.25 Hence x_2 =12-7,25=4.75 \end{eqnarray*}$$

Travel times are

$$\begin{eqnarray*} t_1=12+3\times7.25=33.75 t_2=10+5\times4.75=33.75 i.e. t_1=t_2 \end{eqnarray*}$$

It follows that the travel times are at user equilibrium.

Bibliography