Traffic stream models

Lecture notes in Transportation Systems Engineering

December 10, 2010

Overview

To figure out the exact relationship between the traffic parameters, a great deal of research has been done over the past several decades. The results of these researches yielded many mathematical models. Some important models among them will be discussed in this chapter.

Greenshield's macroscopic stream model

Macroscopic stream models represent how the behaviour of one parameter of traffic flow changes with respect to another. Most important among them is the relation between speed and density. The first and most simple relation between them is proposed by Greenshield. Greenshield assumed a linear speed-density relationship as illustrated in figure 1 to derive the model.

Figure 1: Relation between speed and density

The equation for this relationship is shown below.

$$v = v_f -\left[\frac{v_f}{k_j}\right].k$$ (1)

where $v$ is the mean speed at density $k$, $v_f$ is the free speed and $k_j$ is the jam density. This equation ( 1) is often referred to as the Greenshields' model. It indicates that when density becomes zero, speed approaches free flow speed (ie. $v \rightarrow v_f$ when $k\rightarrow 0$).

Figure 2: Relation between speed and flow

Once the relation between speed and flow is established, the relation with flow can be derived. This relation between flow and density is parabolic in shape and is shown in figure 3. Also, we know that

$$q = k.v$$ (2)

Figure 3: Relation between flow and density 1

Now substituting equation 1 in equation 2, we get

$$q = v_f.k -\left [{\frac{v_f}{k_j}}\right] k^2$$ (3)

Similarly we can find the relation between speed and flow. For this, put $k=\frac{q}{v}$ in equation 1 and solving, we get

$$q = k_j.v -\left[{\frac{k_j}{v_f}}\right] v^2$$ (4)

This relationship is again parabolic and is shown in figure 2. Once the relationship between the fundamental variables of traffic flow is established, the boundary conditions can be derived. The boundary conditions that are of interest are jam density, freeflow speed, and maximum flow. To find density at maximum flow, differentiate equation 3 with respect to $k$ and equate it to zero. ie.,

$$\begin{eqnarray*} \frac{dq}{dk}& = &0\\ v_f - \frac{v_f}{k_j}.2k& = &0 \\ k& =&\frac{k_j}{2}\\ \end{eqnarray*}$$

Denoting the density corresponding to maximum flow as $k_0$,

$$k_0=\frac{k_j}{2}$$ (5)

Therefore, density corresponding to maximum flow is half the jam density Once we get $k_0$, we can derive for maximum flow, $q_{max}$. Substituting equation 5 in equation 3

$$\begin{eqnarray*} q_{max}& =&v_f. \frac {k_j}{2}-\frac{v_f}{k_j}. \left[{\frac{k... ..._f.\frac{k_j}{2} - v_f.\frac{k_j}{4}\\ &=&\frac{{v_f}.{k_j}}{4} \end{eqnarray*}$$

Thus the maximum flow is one fourth the product of free flow and jam density. Finally to get the speed at maximum flow, $v_0$, substitute equation 5 in equation 1 and solving we get,

$$\begin{eqnarray*} v_0& = & v_f - \frac{v_f}{k_j}.\frac{k_j}{2} \end{eqnarray*}$$

$$v_0 = \frac{v_f}{2}$$ (6)

Therefore, speed at maximum flow is half of the free speed.

Calibration of Greenshield's model

Inorder to use this model for any traffic stream, one should get the boundary values, especially free flow speed ($v_f$) and jam density ($k_j$). This has to be obtained by field survey and this is called calibration process. Although it is difficult to determine exact free flow speed and jam density directly from the field, approximate values can be obtained from a number of speed and density observations and then fitting a linear equation between them. Let the linear equation be $y = a + bx$ such that $y$ is density $k$ and $x$ denotes the speed $v$. Using linear regression method, coefficients $a$ and $b$ can be solved as,

$$b = \frac{n\sum_{i=1}^{n}{x_iy_i}-\sum_{i=1}^{n}{x_i}.\sum_{i=1}^{n}{y_i}}{n.\sum_{i=1}^{n}{x_i}^2-({\sum_{i=1}^{n}{x_i}})^2}$$ (7)

$$a = \bar{y}-b\bar{x}$$ (8)

Alternate method of solving for b is,

$$b = \frac{\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^{n}{(x_i - \bar{x})}^2}$$ (9)

where $x_i$ and $y_i$ are the samples, $n$ is the number of samples, and $\bar x$ and $\bar y$ are the mean of $x_i$ and $y_i$ respectively.

Problem

For the following data on speed and density, determine the parameters of the Greenshields' model. Also find the maximum flow and density corresponding to a speed of 30 km/hr.

k	v
171	5
129	15
20	40
70	25

Solution

Denoting y = v and x = k, solve for a and b using equation 8 and equation 9. The solution is tabulated as shown below.

x(k)	y(v)	($x_i-\bar{x}$)	($y_i-\bar{y}$)	($x_i-\bar{x}$)($y_i-\bar{y}$)	( $x_i-\bar{x}^{2}$)
171	5	73.5	-16.3	-1198.1	5402.3
129	15	31.5	-6.3	-198.5	992.3
20	40	-77.5	18.7	-1449.3	6006.3
70	25	-27.5	3.7	-101.8	756.3
390	85			-2947.7	13157.2

$\bar{x} =\frac{\Sigma{x}}{n} =\frac{390}{4}$ = 97.5, $\bar{y} = \frac{\Sigma{y}}{n} = \frac{85}{4}$ = 21.3. From equation 9, b = $\frac{-2947.7}{13157.2}$ = -0.2 $a = y - b\bar{x}$ = 21.3 + 0.2$\times$97.5 = 40.8 So the linear regression equation will be,

$$v = 40.8 - 0.2 k$$ (10)

Here $v_f$ = 40.8 and $\frac{v_f}{k_j}$ = 0.2 This implies, $k_j = \frac{40.8}{0.2}$ = 204 veh/km The basic parameters of Greenshield's model are free flow speed and jam density and they are obtained as 40.8 kmph and 204 veh/km respectively. To find maximum flow, use equation 6, i.e., $q_{max} = \frac{40.8 \times 204}{4}$ = 2080.8 veh/hr Density corresponding to the speed 30 km/hr can be found out by substituting $v = 30$ in equation 10. i.e, 30 = 40.8 - 0.2 $\times$ k Therefore, k = $\frac{40.8 - 30}{0.2}$ = 54 veh/km

Other macroscopic stream models

In Greenshield's model, linear relationship between speed and density was assumed. But in field we can hardly find such a relationship between speed and density. Therefore, the validity of Greenshields' model was questioned and many other models came up. Prominent among them are Greenberg's logarithmic model, Underwood's exponential model, Pipe's generalized model, and multiregime models. These are briefly discussed below.

Greenberg's logarithmic model

Greenberg assumed a logarithmic relation between speed and density. He proposed,

Figure 4: Greenberg's logarithmic model

$$v = v_0 \ln \frac{k_j}{k}$$ (11)

This model has gained very good popularity because this model can be derived analytically. (This derivation is beyond the scope of this notes). However, main drawbacks of this model is that as density tends to zero, speed tends to infinity. This shows the inability of the model to predict the speeds at lower densities.

Underwood's exponential model

Trying to overcome the limitation of Greenberg's model, Underwood put forward an exponential model as shown below.

$$v = v_f.e^\frac{-k}{k_0}$$ (12)

where $v_f$The model can be graphically expressed as in figure 5. is the free flow speedm and $k_o$ is the optimum density, i.e. the densty corresponding to the maximum flow.

Figure 5: Underwood's exponential model

In this model, speed becomes zero only when density reaches infinity which is the drawback of this model. Hence this cannot be used for predicting speeds at high densities.

Pipes' generalized model

Further developments were made with the introduction of a new parameter (n) to provide for a more generalised modelling approach. Pipes proposed a model shown by the following equation.

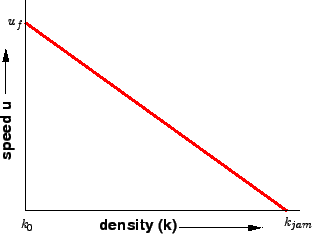
$$v = v_f{[1-{{\left(\frac{k}{k_j}\right)}^n}]}$$ (13)

When $n$ is set to one, Pipe's model resembles Greenshields' model. Thus by varying the values of $n$, a family of models can be developed.

Multiregime models

All the above models are based on the assumption that the same speed-density relation is valid for the entire range of densities seen in traffic streams. Therefore, these models are called single-regime models. However, human behaviour will be different at different densities. This is corraborated with field observations which shows different relations at different range of densities. Therefore, the speed-density relation will also be different in different zones of densities. Based on this concept, many models were proposed generally called multi-regime models. The most simple one is called a two-regime model, where separate equations are used to represent the speed-density relation at congested and uncongested traffic.

Shock waves

The flow of traffic along a stream can be considered similar to a fluid flow. Consider a stream of traffic flowing with steady state conditions, i.e., all the vehicles in the stream are moving with a constant speed, density and flow. Let this be denoted as state A (refer figure 6. Suddenly due to some obstructions in the stream (like an accident or traffic block) the steady state characteristics changes and they acquire another state of flow, say state B. The speed, density and flow of state A is denoted as $v_A$, $k_A$, and $q_A$, and state B as $v_B$, $k_B$, and $q_B$ respectively.

Figure 6: Shock wave: Stream characteristics

The flow-density curve is shown in figure 7.

Figure 7: Shock wave: Flow-density curve

The speed of the vehicles at state A is given by the line joining the origin and point A in the graph. The time-space diagram of the traffic stream is also plotted in figure 8.

Figure 8: Shock wave : time-distance diagram

All the lines are having the same slope which implies that they are moving with constant speed. The sudden change in the characteristics of the stream leads to the formation of a shock wave. There will be a cascading effect of the vehicles in the upstream direction. Thus shock wave is basically the movement of the point that demarcates the two stream conditions. This is clearly marked in the figure 7. Thus the shock waves produced at state B are propagated in the backward direction. The speed of the vehicles at state B is the line joining the origin and point B of the flow-density curve. Slope of the line AB gives the speed of the shock wave (refer figure 7). If speed of the shock-wave is represented as$\omega_{AB}$, then

$$\omega_{AB} = \frac{q_A-q_B}{k_A-k_B}$$ (14)

The above result can be analytically solved by equating the expressions for the number vehicles leaving the upstream and joining the downstream of the shock wave boundary (this assumption is true since the vehicles cannot be created or destroyed. Let $N_A$ be the number of vehicles leaving the section A. Then, $N_A=q_B t$. The relative speed of these vehicles with respect to the shock wave will be $v_A-\omega_{AB}$. Hence,

$$N_A=k_A (v_A-\omega_{AB}) t$$ (15)

Similarly, the vehicles entering the state B is given as

$$N_B=k_A (v_B-\omega_{AB}) t$$ (16)

Equating equations 15 and 16, and solving for $\omega_{AB}$ as follows will yeild to:

$$\begin{eqnarray*} N_A&=&N_B\\ k_A (v_A-\omega_{AB}) t&=&k_B (v_B-\omega_{AB}) t... ...a_{AB} t&=&k_A v_A-k_B v_B\\ \omega_{AB} (k_A-k_B)&=&q_A-q_B\\ \end{eqnarray*}$$

This will yeild the following expression for the shock-wave speed.

$$\omega_{AB} = \frac{q_A-q_B}{k_A-k_B}$$ (17)

In this case, the shock wave move against the direction of traffic and is therefore called a backward moving shock wave. There are other possibilities of shockwaves such as forward moving shockwaves and stationary shockwaves. The forward moving shockwaves are formed when a stream with higher density and higher flow meets a stream with relatively lesser density and flow. For example, when the width of the road increases suddenly, there are chances for a forward moving shockwave. Stationary shockwaves will occur when two streams having the same flow value but different densities meet.

Macroscopic flow models

If one looks into traffic flow from a very long distance, the flow of fairly heavy traffic appears like a stream of a fluid. Therefore, a macroscopic theory of traffic can be developed with the help of hydrodynamic theory of fluids by considering traffic as an effectively one-dimensional compressible fluid. The behaviour of individual vehicle is ignored and one is concerned only with the behaviour of sizable aggregate of vehicles. The earliest traffic flow models began by writing the balance equation to address vehicle number conservation on a road. Infact, all traffic flow models and theories must satisfy the law of conservation of the number of vehicles on the road. Assuming that the vehicles are flowing from left to right, the continuity equation can be written as

$$\frac{\partial k(x,t)}{\partial t} + \frac{\partial q(x,t)}{\partial x} = 0$$ (18)

where $x$ denotes the spatial coordinate in the direction of traffic flow, $t$ is the time, $k$ is the density and $q$ denotes the flow. However, one cannot get two unknowns, namely $k(x,t)$ by and $q(x,t)$ by solving one equation. One possible solution is to write two equations from two regimes of the flow, say before and after a bottleneck. In this system the flow rate before and after will be same, or

$$k_1v_1=k_2v_2$$ (19)

From this the shockwave velocity can be derived as

$$v(t_o)_p = \frac{q_2-q_1}{k_2-k_1}$$ (20)

This is normally referred to as Stock's shockwave formula. An alternate possibility which Lighthill and Whitham adopted in their landmark study is to assume that the flow rate $q$ is determined primarily by the local density $k$, so that flow $q$ can be treated as a function of only density $k$. Therefore the number of unknown variables will be reduced to one. Essentially this assumption states that k(x,t) and q (x,t) are not independent of each other. Therefore the continuity equation takes the form

$$\frac{\partial k(x,t)}{\partial t} + \frac{\partial q (k(x,t))}{\partial x} = 0$$ (21)

However, the functional relationship between flow $q$ and density $k$ cannot be calculated from fluid-dynamical theory. This has to be either taken as a phenomenological relation derived from the empirical observation or from microscopic theories. Therefore, the flow rate $q$ is a function of the vehicular density k; $q = q(k)$. Thus, the balance equation takes the form

$$\frac{\partial k(x,t)}{\partial t} + \frac{\partial q (k(x,t))}{\partial x} = 0$$ (22)

Now there is only one independent variable in the balance equation, the vehicle density $k$. If initial and boundary conditions are known, this can be solved. Solution to LWR models are kinematic waves moving with velocity

$$\frac{dq(k)}{dk}$$ (23)

This velocity $v_k$ is positive when the flow rate increases with density, and it is negative when the flow rate decreases with density. In some cases, this function may shift from one regime to the other, and then a shock is said to be formed. This shockwave propagate at the velocity

$$v_s = \frac{q(k_2) - q(k_1)}{k_2-k_1}$$ (24)

where $q(k_2)$ and $q(k_1)$ are the flow rates corresponding to the upstream density $k_2$ and downstream density $k_1$ of the shockwave. Unlike Stock's shockwave formula there is only one variable here.

Extented Topics

1. Multi regine model (formulation of both two and three regime models)
2. Catastrophe Theory
3. Three dimentional models and plots

Summary

Traffic stream models attempt to establish a better relationship between the traffic parameters. These models were based on many assumptions, for instance, Greenshield's model assumed a linear speed-density relationship. Other models were also discussed in this chapter. The models are used for explaining several phenomena in connection with traffic flow like shock wave.

Problems

1. Stationary shockwaves will occur
   1. when two streams having the same flow value but different densities meet.
   2. when two streams having the different flow value but same densities meet.
   3. when two streams having the same flow value and densities meet.
   4. when two streams with different speeds meet.
2. Linear relationship between speed and density was assumed in
   1. Greenberg's model
   2. Greenshield's model
   3. Pipe's generalized model
   4. Underwood's model

Solutions

1. Stationary shockwaves will occur when two streams having the same flow value but different densities meet.
2. Linear relationship between speed and density was assumed in Greenshield's model

Bibliography

1 Adolf D. May. Fundamentals of Traffic Flow. Prentice - Hall, Inc. Englewood Cliff New Jersey 07632, second edition, 1990.