Transportation networks
Lecture notes in Transportation Systems Engineering
4 August 2009
The conservation equation for a network can be written as:
where,  denote the flow value, and
denote the flow value, and 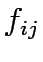 is the flow on link i,j.
is the flow on link i,j.
The net flow across any cut-set 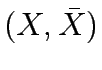 separating the origin and destination is equal to the flow value.
separating the origin and destination is equal to the flow value.
The conservation equation can be conveniently represented in a matrix form.
The node-link incidence matrix in an 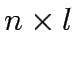 matrix
matrix 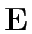 where the rows
corresponds to nodes (
where the rows
corresponds to nodes (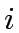 )and the column corresponds to links
)and the column corresponds to links 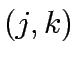 and each
cell denoted by
and each
cell denoted by  defined as:
defined as:
For example ...
The flow conservation equations () can now be written as:
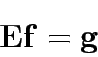 |
(1) |
where 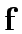 is the vector of link flows,
is the vector of link flows, 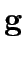 is the O-D vector.
is the O-D vector.
In a connected weighted graph, all spanning trees have n-1 edges and will have minimum or maximum sum of the weights.
Tow algorithms are proposed: Prims algorithma dn Kruskal's algorithm.
`
Prims algorithm grows a spanning tree from a given vertex of a connected
weighted graph G, iteratively adding the cheapest edge from a vertex already
reached to a vertex not yet reached, finishing when all the vertices of G have
been reached.
Break tie arbitrarily.
Input: A weighted, connected graph G(N,L)
Initilisation: T(G)=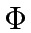 Iteration: Add cheapest edge that incorporate a new vertex
Iteration: Add cheapest edge that incorporate a new vertex
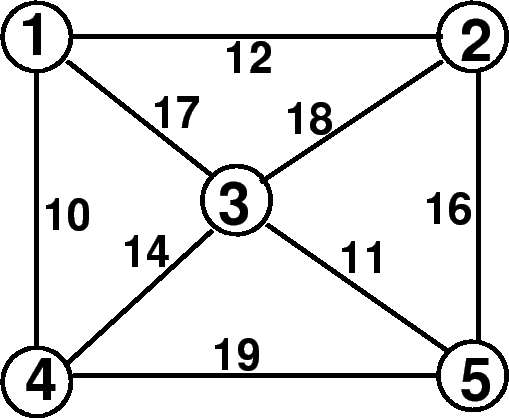
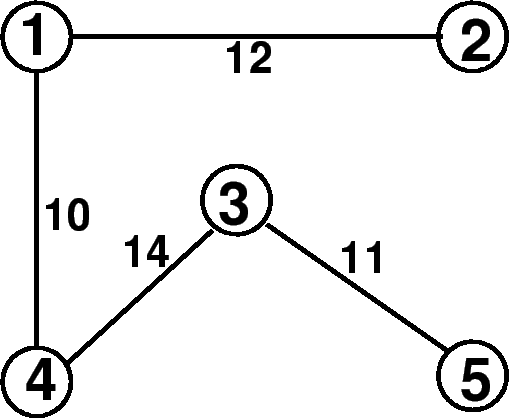
Find the minimum spanning tree of the network given in figure 1
Figure 1:
Example netowrk for minimum spanning tree problem 1
 |
- Start with node 1, N={1}, T={
 }
}
- Node 1 can be connected by nodes 2, 3, and 4, having weights 12, 17, and 10
- Minimim weight is 10, for node 4. So N={1,4}, T={(1,4)}
- Node 1 can be connected by nodes 2 and 3, having weights 12 and 17
- Node 4 can be connected by nodes 3 and 5, having weights 14 and 19
- Minimim weight is 12, for node 2. So N={1,4,2}, T={(1,4),(1,2)}
- Node 1 can be connected by node 3, having weight 17
- Node 4 can be connected by nodes 3 and 5, having weights 14 and 19
- Node 2 can be connected by nodes 3 and 5, having weights 18 and 16
- Minimim weight is 14, for node 3. So N={1,4,2,3}, T={(1,4),(1,2),(3,4)}
- Node 1 can be connected by no nodes without loop
- Node 4 can be connected by node 5, having weight 19
- Node 2 can be connected by node 5, having weight 16
- Node 3 can be connected by node 5, having weight 11
- Minimim weight is 11, for node 3. So N={1,4,2,3}, T={(1,4),(1,2),(3,4),(3,5)} W=49.
Figure 2:
Solution for the example netowrk for minimum spanning tree problem 1
 |
The main concept of this algorithm is to maintain an acyclic spanning sub-graph H, enlargin it by edges with low weight to form a spanning tree.
Consider edges in non-descending order of weight, breaking ties arbitrarily.
Input: A weighted connected graph G(N,L)
Initilization: Set T=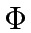 a sub-graph of G
Iteration: If the next cheapest edge joins two components of T, then include it, otherwise, discard it.
Terminate when T is connected.
a sub-graph of G
Iteration: If the next cheapest edge joins two components of T, then include it, otherwise, discard it.
Terminate when T is connected.
Find the minimum spanning tree of the network given in figure 1
- Sort the links in the descending order of weights reslts in
- 19 (4,5); 18 (2,3); 17 (1,3); 16 (2,5); 14 (3,4); 12 (1,2); 11 (3,5); and 10 (1,4)
- T=(1,4) W=10
- T=(1,4),(3,5) W=10+11
- T=(1,4),(3,5),(1,2), W=10+11+12
- T=(1,4),(3,5),(1,2),(3,4), W=10+11+12+14=47
Input: A graph with nonnegative edge weights and a starting vertex 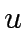 .
The weight of
.
The weight of  is
is  ; let
; let 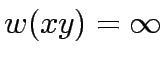 if
if 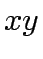 is not an edge.
Initilization: Set
is not an edge.
Initilization: Set
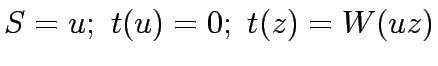 for
for 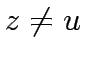 Iteration: Select a vertex
Iteration: Select a vertex 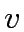 outside
outside 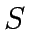 such that
such that
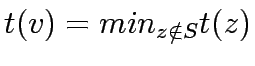 Add
Add 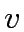 to
to 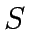 .
Explore edges from
.
Explore edges from 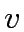 to update tentative distances: for each edge
to update tentative distances: for each edge 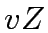 with
with 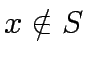 , update
, update 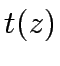 to minimize
to minimize
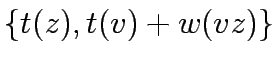 Iteration continues until
Iteration continues until 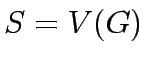 or until
or until 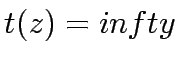 for every
for every 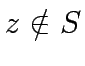 .
At the end, set
.
At the end, set

Table 1:
Solution to the shortest path algorithm
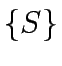 |
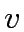 |
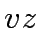 |
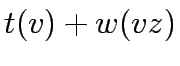 |
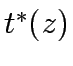 |
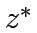 |
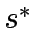 |
| u |
u |
ua |
0+1=1 |
1 |
a |
ua |
| |
|
ub |
0+3=3 |
|
|
|
| ua |
u |
ub |
0+3=3 |
3 |
b |
uab |
| |
a |
ad |
1+5=6 |
|
|
|
| |
|
ac |
1+4=4 |
|
|
|
| uab |
a |
ad |
1+5=6 |
|
|
|
| |
|
ac |
1+4=5 |
5 |
c |
uabc |
| |
b |
bd |
3+4=7 |
|
|
|
| |
|
bc |
3+5=8 |
|
|
|
| uabc |
a |
ad |
|
6 |
d |
uabcd |
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| uabcd |
|
|
|
|
|
uabcdv |
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
- 1
Renfrey B Potts and Robert M Oliver.
Flows in transportation networks.
Academic Press, New York, 1972.
- 2
Douglas B West.
Introduction to graph theory.
Pearson education Asia, New Delhi, India, 2001.
Prof. Tom V. Mathew
2009-08-04
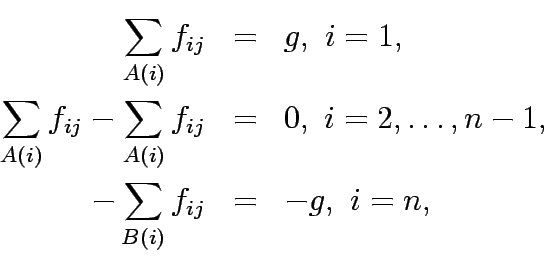
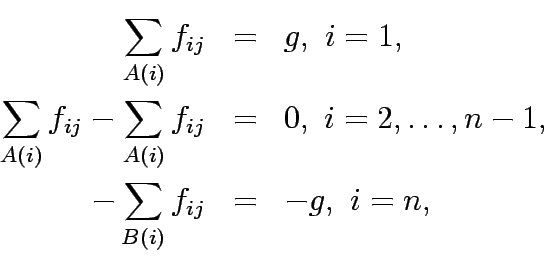
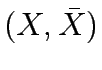 separating the origin and destination is equal to the flow value.
separating the origin and destination is equal to the flow value.
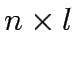 matrix
matrix ![]() where the rows
corresponds to nodes (
where the rows
corresponds to nodes (![]() )and the column corresponds to links
)and the column corresponds to links 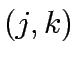 and each
cell denoted by
and each
cell denoted by ![]() defined as:
defined as:
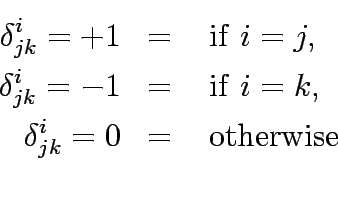
![\begin{eqnarray*}
{\bf E}=\left[
\begin{array}{cccccc}
1 & 1 & 0 & 0 & 0 & 0 ...
...-1 & 0 & 1 & 1 \\
0 & 0 & 0 &-1 & 0 &-1 \\
\end{array}\right]
\end{eqnarray*}](img11.gif)
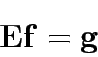
![]() a sub-graph of G
Iteration: If the next cheapest edge joins two components of T, then include it, otherwise, discard it.
Terminate when T is connected.
a sub-graph of G
Iteration: If the next cheapest edge joins two components of T, then include it, otherwise, discard it.
Terminate when T is connected.
 ; let
; let  if
if 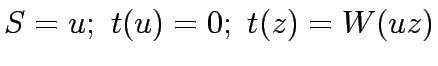 for
for 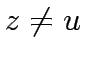 Iteration: Select a vertex
Iteration: Select a vertex 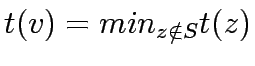 Add
Add 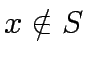 , update
, update 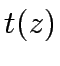 to minimize
to minimize
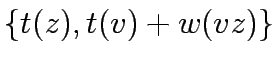 Iteration continues until
Iteration continues until 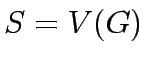 or until
or until 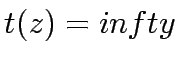 for every
for every 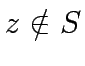 .
At the end, set
.
At the end, set
