Flexible pavement design
Lecture notes in Transportation Systems Engineering
3 August 2009
Flexible pavements are so named because the total pavement structure deflects,
or flexes, under loading.
A flexible pavement structure is typically composed of several layers of
materials.
Each layer receives loads from the above layer, spreads them out, and passes on
these loads to the next layer below.
Thus the stresses will be reduced, which are maximum at the top layer and
minimum on the top of subgrade.
In order to take maximum advantage of this property, layers are usually
arranged in the order of descending load bearing capacity with the highest load
bearing capacity material (and most expensive) on the top and the lowest load
bearing capacity material (and least expensive) on the bottom.
For flexible pavements, structural design is mainly concerned with determining
appropriate layer thickness and composition.
The main design factors are stresses due to traffic load and temperature
variations.
Two methods of flexible pavement structural design are common today:
Empirical design and mechanistic empirical design.
An empirical approach is one which is based on the results of experimentation
or experience.
Some of them are either based on physical properties or strength parameters of
soil subgrade.
An empirical approach is one which is based on the results of experimentation
or experience.
An empirical analysis of flexible pavement design can be done with or with out
a soil strength test.
An example of design without soil strength test is by using
HRB soil classification system, in which soils are grouped from A-1 to A-7
and a group index is added to differentiate soils within each group.
Example with soil strength test uses
McLeod, Stabilometer, California Bearing Ratio (CBR) test.
CBR test is widely known and will be discussed.
Empirical-Mechanistic method of design is based on the mechanics of materials
that relates input, such as wheel load, to an output or pavement response.
In pavement design, the responses are the stresses, strains, and deflections
within a pavement structure and the physical causes are the loads and material
properties of the pavement structure.
The relationship between these phenomena and their physical causes are
typically described using some mathematical models.
Along with this mechanistic approach, empirical elements are used when defining
what value of the calculated stresses, strains, and deflections result in
pavement failure.
The relationship between physical phenomena and pavement failure is described
by empirically derived equations that compute the number of loading cycles to
failure.
There are three different approaches for considering vehicular and traffic
characteristics, which affects pavement design.
Fixed traffic: Thickness of pavement is governed by single load and
number of load repetitions is not considered.
The heaviest wheel load anticipated is used for design purpose.
This is an old method and is rarely used today for pavement design.
Fixed vehicle: In the fixed vehicle procedure, the thickness is governed
by the number of repetitions of a standard axle load.
If the axle load is not a standard one, then it must be converted to an
equivalent axle load by number of repetitions of given axle load and its
equivalent axle load factor.
Variable traffic and vehicle: In this approach, both traffic and vehicle
are considered individually, so there is no need to assign an equivalent factor
for each axle load.
The loads can be divided into a number of groups and the stresses, strains,
and deflections under each load group can be determined separately; and used
for design purposes.
The traffic and loading factors to be considered include axle loads, load
repetitions, and tyre contact area.
To carry maximum load with in the specified limit and to carry greater load,
dual wheel, or dual tandem assembly is often used.
Equivalent single wheel load (ESWL) is the single wheel load having the same
contact pressure, which produces same value of maximum stress, deflection,
tensile stress or contact pressure at the desired depth.
The procedure of finding the ESWL for equal stress criteria is provided below.
This is a semi-rational method, known as Boyd and Foster method, based on the
following assumptions:
- equalancy concept is based on equal stress;
- contact area is circular;
- influence angle is 45
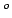 ; and
; and
- soil medium is elastic, homogeneous, and isotropic half space.
The ESWL is given by:
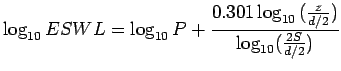 |
|
|
(1) |
where 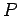 is the wheel load,
is the wheel load, 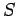 is the center to center distance between the
two wheels,
is the center to center distance between the
two wheels, 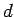 is the clear distance between two wheels, and
is the clear distance between two wheels, and 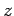 is the
desired depth.
is the
desired depth.
Figure:
ESWL-Equal stress concept
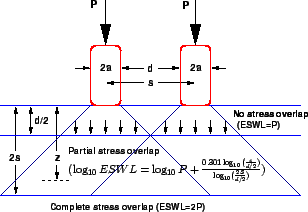 |
Find ESWL at depths of 5cm, 20cm and 40cm for a dual wheel carrying 2044
kg each.
The center to center tyre spacing is 20cm and distance between the walls of the
two tyres is 10cm.
For desired depth z=40cm, which is twice the tyre spacing, ESWL = 2P=2 2044
= 4088 kN.
For z=5cm, which is half the distance between the walls of the tyre, ESWL = P = 2044kN.
For z=20cm,
2044
= 4088 kN.
For z=5cm, which is half the distance between the walls of the tyre, ESWL = P = 2044kN.
For z=20cm,
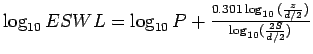 =
=
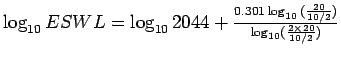 =3.511.
Therefore, ESWL = antilog(3.511)= 3244.49 kN
Vehicles can have many axles which will distribute the load into different
axles, and in turn to the pavement through the wheels.
A standard truck has two axles, front axle with two wheels and rear axle with
four wheels.
But to carry large loads multiple axles are provided.
Since the design of flexible pavements is by layered theory, only the wheels on
one side needed to be considered. On the other hand, the design of rigid
pavement is by plate theory and hence the wheel load on both sides of axle need
to be considered.
Legal axle load: The maximum allowed axle load on the roads is called
legal axle load.
For highways the maximum legal axle load in India, specified by IRC, is 10
tonnes.
Standard axle load: It is a single axle load with dual wheel carrying
80 KN load and the design of pavement is based on the standard axle load.
=3.511.
Therefore, ESWL = antilog(3.511)= 3244.49 kN
Vehicles can have many axles which will distribute the load into different
axles, and in turn to the pavement through the wheels.
A standard truck has two axles, front axle with two wheels and rear axle with
four wheels.
But to carry large loads multiple axles are provided.
Since the design of flexible pavements is by layered theory, only the wheels on
one side needed to be considered. On the other hand, the design of rigid
pavement is by plate theory and hence the wheel load on both sides of axle need
to be considered.
Legal axle load: The maximum allowed axle load on the roads is called
legal axle load.
For highways the maximum legal axle load in India, specified by IRC, is 10
tonnes.
Standard axle load: It is a single axle load with dual wheel carrying
80 KN load and the design of pavement is based on the standard axle load.
Repetition of axle loads:
The deformation of pavement due to a single application of axle load may be
small but due to repeated application of load there would be accumulation of
unrecovered or permanent deformation which results in failure of pavement.
If the pavement structure fails with 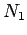 number of repetition of load
number of repetition of load 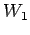 and for the same failure criteria if it requires
and for the same failure criteria if it requires 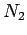 number of repetition of
load
number of repetition of
load 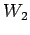 , then
, then 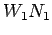 and
and 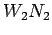 are considered equivalent.
Note that,
are considered equivalent.
Note that, 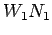 and
and 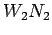 equivalency depends on the failure criterion
employed.
equivalency depends on the failure criterion
employed.
Equivalent axle load factor: An equivalent axle load factor (EALF)
defines the damage per pass to a pavement by the 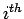 type of axle relative
to the damage per pass of a standard axle load.
While finding the EALF, the failure criterion is important.
Two types of failure criterias are commonly adopted: fatigue cracking and
ruttings.
The fatigue cracking model has the following form:
type of axle relative
to the damage per pass of a standard axle load.
While finding the EALF, the failure criterion is important.
Two types of failure criterias are commonly adopted: fatigue cracking and
ruttings.
The fatigue cracking model has the following form:
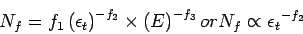 |
(2) |
where, 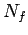 is the number of load repetition for a certain percentage of
cracking,
is the number of load repetition for a certain percentage of
cracking, 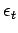 is the tensile strain at the bottom of the binder
course,
is the tensile strain at the bottom of the binder
course, 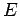 is the modulus of elasticity, and
is the modulus of elasticity, and
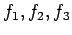 are
constants.
If we consider fatigue cracking as failure criteria, and a typical value of 4
for
are
constants.
If we consider fatigue cracking as failure criteria, and a typical value of 4
for 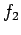 , then:
, then:
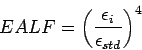 |
(3) |
where, 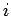 indicate
indicate 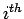 vehicle, and
vehicle, and 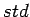 indicate the standard axle.
Now if we assume that the strain is proportional to the wheel load,
indicate the standard axle.
Now if we assume that the strain is proportional to the wheel load,
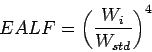 |
(4) |
Similar results can be obtained if rutting model is used, which is:
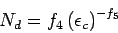 |
(5) |
where 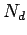 is the permissible design rut depth (say 20mm),
is the permissible design rut depth (say 20mm), 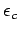 is the
compressive strain at the top of the subgrade, and
is the
compressive strain at the top of the subgrade, and 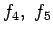 are constants.
Once we have the EALF, then we can get the ESAL as given below.
are constants.
Once we have the EALF, then we can get the ESAL as given below.
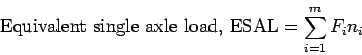 |
(6) |
where,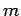 is the number of axle load groups,
is the number of axle load groups,
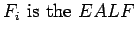 for
for
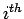 axle load group, and
axle load group, and 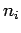 is the number of passes of
is the number of passes of 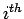 axle
load group during the design period.
Let number of load repetition expected by 80 KN standard axle is 1000, 160 KN
is 100 and 40 KN is 10000.
Find the equivalent axle load.
Refer the Table
axle
load group during the design period.
Let number of load repetition expected by 80 KN standard axle is 1000, 160 KN
is 100 and 40 KN is 10000.
Find the equivalent axle load.
Refer the Table ![[*]](file:/usr/share/latex2html/icons/crossref.gif) . The ESAL is given as
. The ESAL is given as
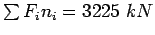
Table:
Example 1 Solution
| |
Axle |
No.of Load |
EALF |
|
| |
Load |
Repetition |
|
|
| i |
(KN) |
(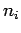 ) ) |
(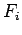 ) ) |
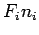 |
| 1 |
40 |
10000 |
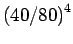 = 0.0625 = 0.0625 |
625 |
| 2 |
80 |
1000 |
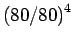 = 1 = 1 |
1000 |
| 3 |
160 |
100 |
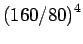 = 16 = 16 |
1600 |
Let the number of load repetition expected by 120 kN axle is 1000, 160 kN
is 100, and 40 kN is 10,000.
Find the equivalent standard axle load if the equivalence criteria is rutting.
Assume 80 kN as standard axle load and the rutting model is
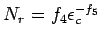 where
where 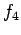 =4.2 and
=4.2 and 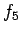 =4.5.
Refer the Table
=4.5.
Refer the Table ![[*]](file:/usr/share/latex2html/icons/crossref.gif) . The ESAL is given as
. The ESAL is given as
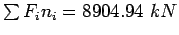
Table:
Example 2 Solution
| |
Axle |
No.of Load |
EALF |
|
| |
Load |
Repetition |
|
|
| i |
(KN) |
(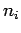 ) ) |
(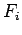 ) ) |
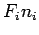 |
| 1 |
120 |
1000 |
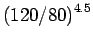 = 6.200 = 6.200 |
6200 |
| 2 |
160 |
100 |
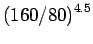 = 22.63 = 22.63 |
2263 |
| 3 |
40 |
10000 |
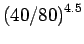 = 0.04419 = 0.04419 |
441.9 |
Let number of load repetition expected by 60kN standard axle is 1000,
120kN is 200 and 40 kN is 10000.
Find the equivalent axle load using fatigue cracking as failure criteria
according to IRC.
Hint:
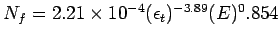 Refer the Table
Refer the Table ![[*]](file:/usr/share/latex2html/icons/crossref.gif) . The ESAL is given as
. The ESAL is given as
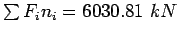
Table:
Example 3 Solution
| |
Axle |
No.of Load |
EALF |
|
| |
Load |
Repetition |
|
|
| i |
(KN) |
( ) ) |
(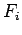 ) ) |
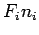 |
| 1 |
40 |
10000 |
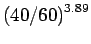 = 0.2065 = 0.2065 |
2065 |
| 2 |
60 |
1000 |
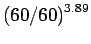 = 1 = 1 |
1000 |
| 3 |
120 |
200 |
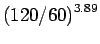 = 14.825 = 14.825 |
2965.081 |
It is well known that the pavement materials are not perfectly elastic but
experiences some permanent deformation after each load repetitions.
It is well known that most paving materials are not elastic but experience some
permanent deformation after each load application.
However, if the load is small compared to the strength of the material and the deformation under each load
repetition is almost completely recoverable then the material can be considered as elastic.
The Figure ![[*]](file:/usr/share/latex2html/icons/crossref.gif) shows straining of a specimen under a repeated
load test.
At the initial stage of load applications, there is considerable permanent
deformation as indicated by the plastic strain in the
Figure
shows straining of a specimen under a repeated
load test.
At the initial stage of load applications, there is considerable permanent
deformation as indicated by the plastic strain in the
Figure ![[*]](file:/usr/share/latex2html/icons/crossref.gif) .
As the number of repetition increases, the plastic strain due to each load
repetition decreases.
After 100 to 200 repetitions, the strain is practically all-recoverable, as
indicated by
.
As the number of repetition increases, the plastic strain due to each load
repetition decreases.
After 100 to 200 repetitions, the strain is practically all-recoverable, as
indicated by  in the figure.
in the figure.
In pavements the load applied are mostly transient and the type and
duration of loading used in the repeated load test should simulate that
actually occurring in the field.
When a load is at a considerable distance from a given point, the stress at
that point is maximum.
It is therefore reasonable to assume the stress pulse to be a haversine or
triangular loading, and the duration of loading depends on the vehicle speed
and the depth of the point below the pavement surface.
Resilient modulus test can be conducted on all types of pavement materials
ranging from cohesive to stabilized materials.
The test is conducted in a triaxial device equipped for repetitive load
conditions.
The outputs of the layered elastic model are the stresses, strains and
deflections in the pavements.
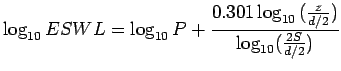
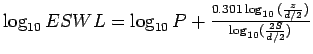 =
=
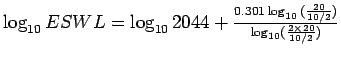 =3.511.
Therefore, ESWL = antilog(3.511)= 3244.49 kN
=3.511.
Therefore, ESWL = antilog(3.511)= 3244.49 kN
![]() number of repetition of load
number of repetition of load ![]() and for the same failure criteria if it requires
and for the same failure criteria if it requires ![]() number of repetition of
load
number of repetition of
load ![]() , then
, then ![]() and
and ![]() are considered equivalent.
Note that,
are considered equivalent.
Note that, ![]() and
and ![]() equivalency depends on the failure criterion
employed.
equivalency depends on the failure criterion
employed.
![]() type of axle relative
to the damage per pass of a standard axle load.
While finding the EALF, the failure criterion is important.
Two types of failure criterias are commonly adopted: fatigue cracking and
ruttings.
The fatigue cracking model has the following form:
type of axle relative
to the damage per pass of a standard axle load.
While finding the EALF, the failure criterion is important.
Two types of failure criterias are commonly adopted: fatigue cracking and
ruttings.
The fatigue cracking model has the following form:
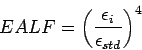
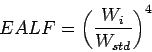
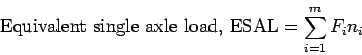
![]() shows straining of a specimen under a repeated
load test.
At the initial stage of load applications, there is considerable permanent
deformation as indicated by the plastic strain in the
Figure
shows straining of a specimen under a repeated
load test.
At the initial stage of load applications, there is considerable permanent
deformation as indicated by the plastic strain in the
Figure ![]() .
As the number of repetition increases, the plastic strain due to each load
repetition decreases.
After 100 to 200 repetitions, the strain is practically all-recoverable, as
indicated by
.
As the number of repetition increases, the plastic strain due to each load
repetition decreases.
After 100 to 200 repetitions, the strain is practically all-recoverable, as
indicated by ![]() in the figure.
in the figure.