Fundamental relations of traffic flow
Lecture notes in Transportation Systems Engineering
August 3, 2010
Speed is one of the basic parameters of traffic flow and time mean speed and
space mean speed are the two representations of speed.
Time mean speed and space mean speed and the relationship between them will be
discussed in detail in this chapter.
The relationship between the fundamental parameters of traffic flow will also
be derived.
In addition, this relationship can be represented in graphical form resulting
in the fundamental diagrams of traffic flow.
As noted earlier, time mean speed is the average of all vehicles passing a
point over a duration of time.
It is the simple average of spot speed.
Time mean speed 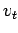 is given by,
is given by,
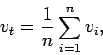 |
(1) |
where 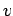 is the spot speed of
is the spot speed of 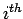 vehicle, and
vehicle, and 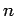 is the number of
observations.
In many speed studies, speeds are represented in the form of frequency table.
Then the time mean speed is given by,
is the number of
observations.
In many speed studies, speeds are represented in the form of frequency table.
Then the time mean speed is given by,
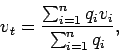 |
(2) |
where 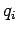 is the number of vehicles having speed
is the number of vehicles having speed 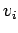 , and
, and 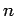 is the number
of such speed categories.
is the number
of such speed categories.
The space mean speed also averages the spot speed, but spatial weightage is
given instead of temporal.
This is derived as below.
Consider unit length of a road, and let 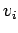 is the spot speed of
is the spot speed of 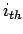 vehicle.
Let
vehicle.
Let 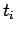 is the time the vehicle takes to complete unit distance and is given
by
is the time the vehicle takes to complete unit distance and is given
by 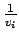 .
If there are
.
If there are 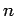 such vehicles, then the average travel time
such vehicles, then the average travel time 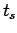 is given by,
is given by,
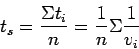 |
(3) |
If 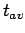 is the average travel time, then average speed
is the average travel time, then average speed
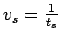 .
Therefore from the above equation,
.
Therefore from the above equation,
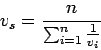 |
(4) |
This is simply the harmonic mean of the spot speed.
If the spot speeds are expressed as a frequency table, then,
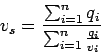 |
(5) |
where 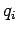 vehicle will have
vehicle will have 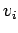 speed and
speed and 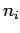 is the number of such
observations.
is the number of such
observations.
If the spot speeds are 50, 40, 60,54 and 45, then find the time mean speed and
space mean speed.
Time mean speed 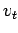 is the average of spot speed.
Therefore,
is the average of spot speed.
Therefore,
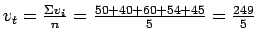 =
49.8
Space mean speed is the harmonic mean of spot speed.Therefore,
=
49.8
Space mean speed is the harmonic mean of spot speed.Therefore,
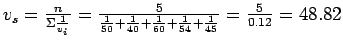
The results of a speed study is given in the form of a frequency distribution
table.
Find the time mean speed and space mean speed.
| speed range |
frequency |
| 2-5 |
1 |
| 6-9 |
4 |
| 10-13 |
0 |
| 14-17 |
7 |
| No. |
speed range |
average speed (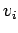 ) ) |
volume of flow (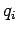 ) ) |
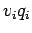 |
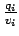 |
| 1 |
2-5 |
3.5 |
1 |
3.5 |
2.29 |
| 2 |
6-9 |
7.5 |
4 |
30.0 |
0.54 |
| 3 |
10-13 |
11.5 |
0 |
0 |
0 |
| 4 |
14-17 |
15.5 |
7 |
108.5 |
0.45 |
| |
total |
|
12 |
142 |
3.28 |
The time mean speed and space mean speed can be found out from the frequency
table given below.
First, the average speed is computed, which is the mean of the speed range.
For example, for the first speed range, average speed,
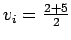 =
3.5 seconds.
The volume of flow
=
3.5 seconds.
The volume of flow 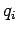 for that speed range is same as the frequency.
The terms
for that speed range is same as the frequency.
The terms 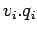 and
and
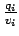 are also tabulated, and their
summations in the last row.
Time mean speed can be computed as,
are also tabulated, and their
summations in the last row.
Time mean speed can be computed as,
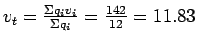 Similarly, space mean speed can be computed as,
Similarly, space mean speed can be computed as,
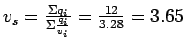
Inorder to understand the concept of time mean speed and space mean speed,
following illustration will help.
Let there be a road stretch having two sets of vehicle as in
figure 1.
Figure 1:
Illustration of relation between time mean speed and space mean speed
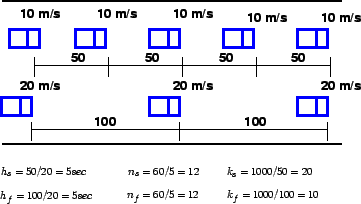 |
The first vehicle is traveling at 10m/s with 50 m spacing, and the second set
at 20m/s with 100 m spacing.
Therefore, the headway of the slow vehicle 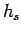 will be 50 m divided by 10 m/s
which is 5 sec.
Therefore, the number of slow moving vehicles observed at A in one hour
will be 50 m divided by 10 m/s
which is 5 sec.
Therefore, the number of slow moving vehicles observed at A in one hour 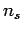 will be 60/5 = 12 vehicles.
The density
will be 60/5 = 12 vehicles.
The density 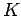 is the number of vehicles in 1 km, and is the inverse of
spacing.
Therefore,
is the number of vehicles in 1 km, and is the inverse of
spacing.
Therefore, 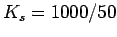 = 20 vehicles/km.
Therefore, by definition, time mean speed
= 20 vehicles/km.
Therefore, by definition, time mean speed 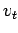 is given by
is given by
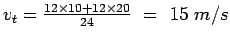 .
Similarly, by definition, space mean speed is the mean of vehicle speeds over
time.
Therefore,
.
Similarly, by definition, space mean speed is the mean of vehicle speeds over
time.
Therefore,
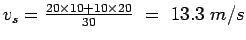 This is same as the harmonic mean of spot speeds obtained at location A; ie
This is same as the harmonic mean of spot speeds obtained at location A; ie
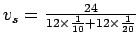 = 13.3 m/s.
It may be noted that since harmonic mean is always lower than the arithmetic
mean, and also as observed , space mean speed is always lower than the time
mean speed.
In other words, space mean speed weights slower vehicles more heavily as they
occupy the road stretch for longer duration of time.
For this reason, in many fundamental traffic equations, space mean speed is
preferred over time mean speed.
= 13.3 m/s.
It may be noted that since harmonic mean is always lower than the arithmetic
mean, and also as observed , space mean speed is always lower than the time
mean speed.
In other words, space mean speed weights slower vehicles more heavily as they
occupy the road stretch for longer duration of time.
For this reason, in many fundamental traffic equations, space mean speed is
preferred over time mean speed.
The relation between time mean speed and space mean speed can be derived as
below.
Consider a stream of vehicles with a set of substream flow 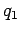 ,
,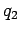 , ...
, ...
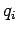 , ...
, ...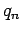 having speed
having speed 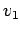 ,
,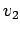 , ...
, ...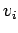 , ...
, ...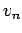 .
The fundamental relation between flow(
.
The fundamental relation between flow(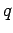 ), density(
), density(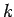 ) and mean speed
) and mean speed 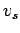 is,
is,
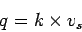 |
(6) |
Therefore for any substream 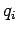 , the following relationship will be valid.
, the following relationship will be valid.
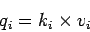 |
(7) |
The summation of all substream flows will give the total flow 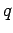 .
.
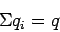 |
(8) |
Similarly the summation of all substream density will give the total density
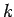 .
.
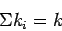 |
(9) |
Let 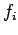 denote the proportion of substream density
denote the proportion of substream density 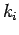 to the total density
to the total density
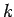 ,
,
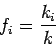 |
(10) |
Space mean speed averages the speed over space.
Therefore, if 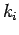 vehicles has
vehicles has 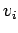 speed, then space mean speed is given
by,
speed, then space mean speed is given
by,
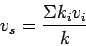 |
(11) |
Time mean speed averages the speed over time.Therefore,
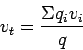 |
(12) |
Substituting in 7 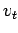 can be written as,
can be written as,
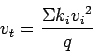 |
(13) |
Rewriting the above equation and substituting 11, and then
substituting 6, we get,
By adding and subtracting 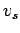 and doing algebraic manipulations,
and doing algebraic manipulations, 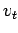 can be
written as,
can be
written as,
The third term of the equation will be zero because
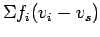 will
be zero, since
will
be zero, since 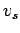 is the mean speed of
is the mean speed of 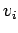 .
The numerator of the second term gives the standard deviation of
.
The numerator of the second term gives the standard deviation of 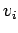 .
.
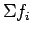 by definition is 1.Therefore,
by definition is 1.Therefore,
Hence, time mean speed is space mean speed plus standard deviation of the spot
speed divided by the space mean speed.
Time mean speed will be always greater than space mean speed since standard
deviation cannot be negative.
If all the speed of the vehicles are the same, then spot speed, time mean speed
and space mean speed will also be same.
The relationship between the fundamental variables of traffic flow, namely
speed, volume, and density is called the fundamental relations of traffic flow.
This can be derived by a simple concept.
Let there be a road with length 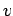 km, and assume all the vehicles are moving
with
km, and assume all the vehicles are moving
with 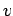 km/hr.(Fig 2).
km/hr.(Fig 2).
Figure 2:
Illustration of relation between fundamental parameters of traffic flow
 |
Let the number of vehicles counted by an observer at A for one hour be 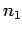 .
By definition, the number of vehicles counted in one hour is flow(q).
Therefore,
.
By definition, the number of vehicles counted in one hour is flow(q).
Therefore,
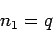 |
(19) |
Similarly, by definition, density is the number of vehicles in unit
distance.
Therefore number of vehicles 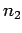 in a road stretch of distance
in a road stretch of distance 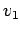 will be
density
will be
density  distance.Therefore,
distance.Therefore,
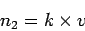 |
(20) |
Since all the vehicles have speed 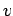 , the number of vehicles counted in 1 hour
and the number of vehicles in the stretch of distance
, the number of vehicles counted in 1 hour
and the number of vehicles in the stretch of distance 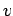 will also be same.(ie
will also be same.(ie
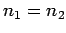 ).
Therefore,
).
Therefore,
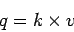 |
(21) |
This is the fundamental equation of traffic flow.
Please note that, 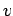 in the above equation refers to the space mean speed.
in the above equation refers to the space mean speed.
The relation between flow and density, density and speed, speed and flow, can
be represented with the help of some curves.
They are referred to as the fundamental diagrams of traffic flow.
They will be explained in detail one by one below.
The flow and density varies with time and location.
The relation between the density and the corresponding flow on a given stretch
of road is referred to as one of the fundamental diagram of traffic flow.
Some characteristics of an ideal flow-density relationship is listed below:
- When the density is zero, flow will also be zero,since there is no
vehicles on the road.
- When the number of vehicles gradually increases the density as well as
flow increases.
- When more and more vehicles are added, it reaches a situation where
vehicles can't move.
This is referred to as the jam density or the maximum density.
At jam density, flow will be zero because the vehicles are not moving.
- There will be some density between zero density and jam density, when the
flow is maximum.
The relationship is normally represented by a parabolic curve as shown in
figure 3
Figure 3:
Flow density curve
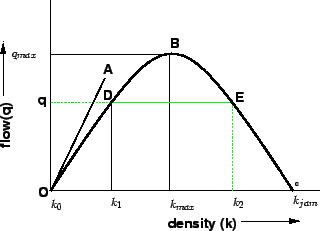 |
The point O refers to the case with zero density and zero flow.
The point B refers to the maximum flow and the corresponding density is
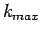 .
The point C refers to the maximum density
.
The point C refers to the maximum density 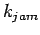 and the corresponding flow
is zero.
OA is the tangent drawn to the parabola at O, and the slope of the line OA
gives the mean free flow speed, ie the speed with which a vehicle can travel
when there is no flow.
It can also be noted that points D and E correspond to same flow but has two
different densities.
Further, the slope of the line OD gives the mean speed at density
and the corresponding flow
is zero.
OA is the tangent drawn to the parabola at O, and the slope of the line OA
gives the mean free flow speed, ie the speed with which a vehicle can travel
when there is no flow.
It can also be noted that points D and E correspond to same flow but has two
different densities.
Further, the slope of the line OD gives the mean speed at density 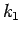 and
slope of the line OE will give mean speed at density
and
slope of the line OE will give mean speed at density 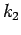 .
Clearly the speed at density
.
Clearly the speed at density 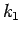 will be higher since there are less number
of vehicles on the road.
will be higher since there are less number
of vehicles on the road.
Similar to the flow-density relationship, speed will be maximum, referred to as
the free flow speed, and when the density is maximum, the speed will be zero.
The most simple assumption is that this variation of speed with density is
linear as shown by the solid line in figure 4.
Corresponding to the zero density, vehicles will be flowing with their desire
speed, or free flow speed.
When the density is jam density, the speed of the vehicles becomes zero.
Figure 4:
Speed-density diagram
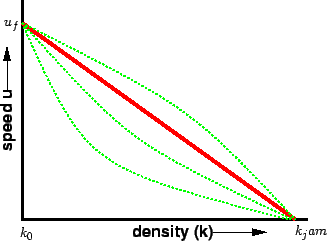 |
It is also possible to have non-linear relationships as shown by the dotted
lines.
These will be discussed later.
The relationship between the speed and flow can be postulated as follows.
The flow is zero either because there is no vehicles or there are too many
vehicles so that they cannot move.
At maximum flow, the speed will be in between zero and free flow speed.
This relationship is shown in figure 5.
Figure 5:
Speed-flow diagram
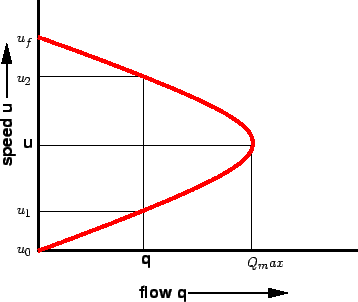 |
The maximum flow 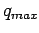 occurs at speed
occurs at speed 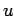 .
It is possible to have two different speeds for a given flow.
.
It is possible to have two different speeds for a given flow.
The diagrams shown in the relationship between speed-flow, speed-density, and
flow-density are called the fundamental diagrams of traffic flow.
These are as shown in figure 6
Figure 6:
Fundamental diagram of traffic flow
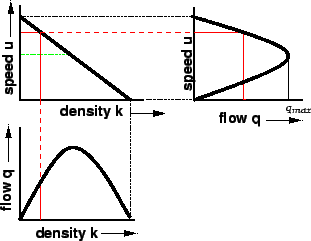 |
Time mean speed and space mean speed are two important measures of speed.
It is possible to have a relation between them and was derived in this chapter.
Also, time mean speed will be always greater than or equal to space mean speed.
The fundamental diagrams of traffic flow are vital tools which enables analysis
of fundamental relationships.
There are three diagrams - speed-density, speed-flow and flow-density.
They can be together combined in a single diagram as discussed in the last
section of the chapter.
- Space mean speed is
- the harmonic mean of spot speeds
- the sum of spot speeds
- the arithmetic mean of spot speeds
- the sum of journey speeds
- Which among the following is the fundamental equation of traffic flow?
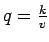
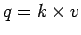
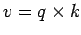
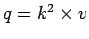
- Space mean speed is
- the harmonic mean of spot speeds
- the sum of spot speeds
- the arithmetic mean of spot speeds
- the sum of journey speeds
- Which among the following is the fundamental equation of traffic flow?
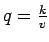
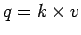
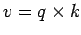
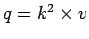
Prof. Tom V. Mathew
2010-08-03
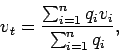
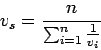
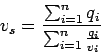
![]() =
3.5 seconds.
The volume of flow
=
3.5 seconds.
The volume of flow ![]() for that speed range is same as the frequency.
The terms
for that speed range is same as the frequency.
The terms ![]() and
and
![]() are also tabulated, and their
summations in the last row.
Time mean speed can be computed as,
are also tabulated, and their
summations in the last row.
Time mean speed can be computed as,
![]() Similarly, space mean speed can be computed as,
Similarly, space mean speed can be computed as,
![]()
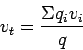
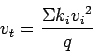
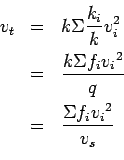
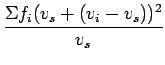
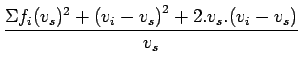
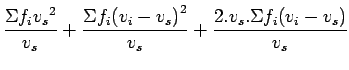
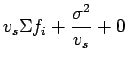
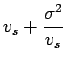
![]() in a road stretch of distance
in a road stretch of distance ![]() will be
density
will be
density ![]() distance.Therefore,
distance.Therefore,