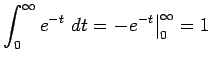 |
(2) |
![\begin{eqnarray*}
p(h\ge t)&=&1-p(h<t)\\
&=&1-p\left[\int_{0}^{h} e^{-t} dt\right]\\
&=&1-\left[\left.-e^{-t}\right\vert^h_0\right]\\
&=&e^{-h}
\end{eqnarray*}](img7.gif)
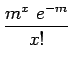 |
(3) |
where
| (4) | |||
| (5) | |||
| (6) |
where
Lecture notes in Transportation Systems Engineering
4 August 2009
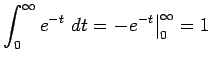 |
(2) |
![\begin{eqnarray*}
p(h\ge t)&=&1-p(h<t)\\
&=&1-p\left[\int_{0}^{h} e^{-t} dt\right]\\
&=&1-\left[\left.-e^{-t}\right\vert^h_0\right]\\
&=&e^{-h}
\end{eqnarray*}](img7.gif)
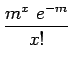 |
(3) |
| (4) | |||
| (5) | |||
| (6) |
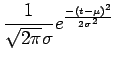 |
(7) |
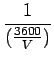 |
(9) |
| (10) | |||
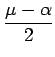 |
(11) |
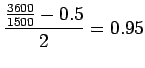 |
(12) |
![$\displaystyle p\left[\frac{t-\mu}{\sigma}\le \frac{h-\mu}{\sigma}\le \frac{(t+\delta t)-\mu}{\sigma}\right]$](img43.gif) |
(13) | ||
![$\displaystyle p\left[h\le \frac{(t+\delta t)-\mu}{\sigma}\right] - p\left[h\le \frac{t-\mu}{\sigma}\right]$](img44.gif) |
(14) |
| (15) | |||
![$\displaystyle p\left[h\le \frac{2.0-2.25}{0.875}\right] - p\left[h\le \frac{1.5-2.25}{0.875}\right]$](img50.gif) |
(16) | ||
| (17) | |||
| (18) | |||
| (19) |
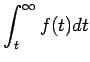 |
(20) |
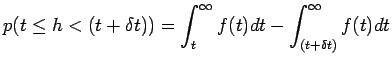 |
(21) |
| t | t+dt | p (obs) |
| 0.0 | 0.5 | 0.012 |
| 0.5 | 1.0 | 0.064 |
| 1.0 | 1.5 | 0.114 |
| 1.5 | 2.0 | 0.159 |
| 2.0 | 2.5 | 0.157 |
| 2.5 | 3.0 | 0.130 |
| 3.0 | 3.5 | 0.088 |
| 3.5 | 4.0 | 0.065 |
| 4.0 | 4.5 | 0.043 |
| 4.5 | 5.0 | 0.033 |
| 5.0 | 5.5 | 0.022 |
| 5.5 | 6.0 | 0.019 |
| 6.0 | 6.5 | 0.014 |
| 6.5 | 7.0 | 0.010 |
| 7.0 | 7.5 | 0.012 |
| 7.5 | 8.0 | 0.008 |
| 8.0 | 8.5 | 0.005 |
| 8.5 | 9.0 | 0.007 |
| 9.0 | 9.5 | 0.005 |
| 9.5 | 0.033 | |
| Total | 1.00 |
| t | t+dt | p (obs) | Pobs=p*N | N-exp (p) | P=p*N | |
| 0.0 | 0.5 | 0.012 | 41.1 | 1.000 | 0.133 | 455.8 |
| 0.5 | 1.0 | 0.064 | 219.1 | 0.867 | 0.115 | 395.1 |
| 1.0 | 1.5 | 0.114 | 390.3 | 0.751 | 0.100 | 342.5 |
| 1.5 | 2.0 | 0.159 | 544.4 | 0.651 | 0.087 | 296.9 |
| 2.0 | 2.5 | 0.157 | 537.6 | 0.565 | 0.075 | 257.4 |
| 2.5 | 3.0 | 0.130 | 445.1 | 0.490 | 0.065 | 223.1 |
| 3.0 | 3.5 | 0.088 | 301.3 | 0.424 | 0.056 | 193.4 |
| 3.5 | 4.0 | 0.065 | 222.6 | 0.368 | 0.049 | 167.7 |
| 4.0 | 4.5 | 0.043 | 147.2 | 0.319 | 0.042 | 145.4 |
| 4.5 | 5.0 | 0.033 | 113.0 | 0.276 | 0.037 | 126.0 |
| 5.0 | 5.5 | 0.022 | 75.3 | 0.240 | 0.032 | 109.2 |
| 5.5 | 6.0 | 0.019 | 65.1 | 0.208 | 0.028 | 94.7 |
| 6.0 | 6.5 | 0.014 | 47.9 | 0.180 | 0.024 | 82.1 |
| 6.5 | 7.0 | 0.010 | 34.2 | 0.156 | 0.021 | 71.2 |
| 7.0 | 7.5 | 0.012 | 41.1 | 0.135 | 0.018 | 61.7 |
| 7.5 | 8.0 | 0.008 | 27.4 | 0.117 | 0.016 | 53.5 |
| 8.0 | 8.5 | 0.005 | 17.1 | 0.102 | 0.014 | 46.4 |
| 8.5 | 9.0 | 0.007 | 24.0 | 0.088 | 0.012 | 40.2 |
| 9.0 | 9.5 | 0.005 | 17.1 | 0.076 | 0.010 | 34.8 |
| 9.5 | 0.033 | 113.0 | 0.066 | 0.066 | 226.8 | |
| Total | 1.000 | 3424 | 1.000 | 3424 |
| h | t+dt | p (obs) | P=p*N | P=p*N | ||
| 0.0 | 0.5 | 0.012 | 41.09 | 0.010 | 0.013 | 44.289 |
| 0.5 | 1.0 | 0.064 | 219.14 | 0.023 | 0.025 | 85.738 |
| 1.0 | 1.5 | 0.114 | 390.34 | 0.048 | 0.043 | 148.673 |
| 1.5 | 2.0 | 0.159 | 544.42 | 0.091 | 0.067 | 230.928 |
| 2.0 | 2.5 | 0.157 | 537.57 | 0.159 | 0.094 | 321.299 |
| 2.5 | 3.0 | 0.13 | 445.12 | 0.252 | 0.117 | 400.433 |
| 3.0 | 3.5 | 0.088 | 301.31 | 0.369 | 0.131 | 447.033 |
| 3.5 | 4.0 | 0.065 | 222.56 | 0.500 | 0.131 | 447.033 |
| 4.0 | 4.5 | 0.043 | 147.23 | 0.631 | 0.117 | 400.433 |
| 4.5 | 5.0 | 0.033 | 112.99 | 0.748 | 0.094 | 321.299 |
| 5.0 | 5.5 | 0.022 | 75.33 | 0.841 | 0.067 | 230.928 |
| 5.5 | 6.0 | 0.019 | 65.06 | 0.909 | 0.043 | 148.673 |
| 6.0 | 6.5 | 0.014 | 47.94 | 0.952 | 0.025 | 85.738 |
| 6.5 | 7.0 | 0.01 | 34.24 | 0.977 | 0.013 | 44.289 |
| 7.0 | 7.5 | 0.012 | 41.09 | 0.990 | 0.006 | 20.492 |
| 7.5 | 8.0 | 0.008 | 27.39 | 0.996 | 0.002 | 8.493 |
| 8.0 | 8.5 | 0.005 | 17.12 | 0.999 | 0.001 | 3.153 |
| 8.5 | 9.0 | 0.007 | 23.97 | 1.000 | 0.000 | 1.048 |
| 9.0 | 9.5 | 0.005 | 17.12 | 1.000 | 0.000 | 0.312 |
| 9.5 | 0.033 | 112.99 | 1.000 | 0.010 | 33.716 | |
| 3424 |
| h | t+dt | p (obs) | P=p*N | f(t) | P=p*N | |
| 0.0 | 0.5 | 0.012 | 41.09 | 0.000 | 0.00 | |
| 0.5 | 1.0 | 0.064 | 219.14 | 0.000 | 0.066 | 225.91 |
| 1.0 | 1.5 | 0.114 | 390.34 | 0.264 | 0.127 | 433.26 |
| 1.5 | 2.0 | 0.159 | 544.42 | 0.242 | 0.114 | 389.45 |
| 2.0 | 2.5 | 0.157 | 537.57 | 0.213 | 0.099 | 339.13 |
| 2.5 | 3.0 | 0.13 | 445.12 | 0.183 | 0.085 | 291.12 |
| 3.0 | 3.5 | 0.088 | 301.31 | 0.157 | 0.072 | 247.86 |
| 3.5 | 4.0 | 0.065 | 222.56 | 0.133 | 0.061 | 209.90 |
| 4.0 | 4.5 | 0.043 | 147.23 | 0.112 | 0.052 | 177.08 |
| 4.5 | 5.0 | 0.033 | 112.99 | 0.095 | 0.044 | 148.97 |
| 5.0 | 5.5 | 0.022 | 75.33 | 0.079 | 0.037 | 125.04 |
| 5.5 | 6.0 | 0.019 | 65.06 | 0.067 | 0.031 | 104.78 |
| 6.0 | 6.5 | 0.014 | 47.94 | 0.056 | 0.026 | 87.67 |
| 6.5 | 7.0 | 0.01 | 34.24 | 0.047 | 0.021 | 73.28 |
| 7.0 | 7.5 | 0.012 | 41.09 | 0.039 | 0.018 | 61.18 |
| 7.5 | 8.0 | 0.008 | 27.39 | 0.033 | 0.015 | 51.04 |
| 8.0 | 8.5 | 0.005 | 17.12 | 0.027 | 0.012 | 42.54 |
| 8.5 | 9.0 | 0.007 | 23.97 | 0.023 | 0.010 | 35.44 |
| 9.0 | 9.5 | 0.005 | 17.12 | 0.019 | 0.009 | 29.51 |
| 9.5 | 0.033 | 112.99 | 0.016 | 0.102 | 350.83 | |
| x | 3424 |