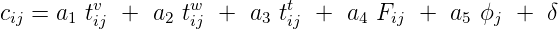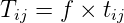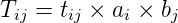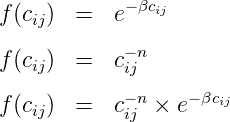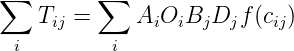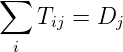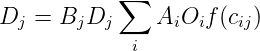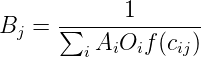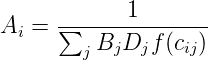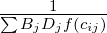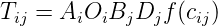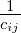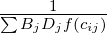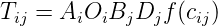Trip Distribution
Lecture Notes in Transportation Systems Engineering
Contents
_________________________________________________________________________________________
1 Overview
The decision to travel for a given purpose is called trip generation. These generated trips from each
zone is then distributed to all other zones based on the choice of destination. This is called trip
distribution which forms the second stage of travel demand modeling. There are a number of methods
to distribute trips among destinations; and two such methods are growth factor model and gravity
model. Growth factor model is a method which respond only to relative growth rates at origins and
destinations and this is suitable for short-term trend extrapolation. In gravity model, we start from
assumptions about trip making behavior and the way it is influenced by external factors.
An important aspect of the use of gravity models is their calibration, that is the task of
fixing their parameters so that the base year travel pattern is well represented by the
model.
2 Definitions and notations
2.1 Trip matrix
The trip pattern in a study area can be represented by means of a trip matrix or origin-destination
(O-D)matrix. This is a two dimensional array of cells where rows and columns represent
each of the zones in the study area. The notation of the trip matrix is given in figure 1.
The cells of each row i contain the trips originating in that zone which have as destinations the
zones in the corresponding columns. Tij is the number of trips between origin i and destination j. Oi
is the total number of trips between originating in zone i and Dj is the total number of trips attracted
to zone j. The sum of the trips in a row should be equal to the total number of trips emanating from
that zone. The sum of the trips in a column is the number of trips attracted to that zone. These two
constraints can be represented as: ∑
jTij = Oi ∑
iTij = Dj If reliable information is available
to estimate both Oi and Dj, the model is said to be doubly constrained. In some cases,
there will be information about only one of these constraints, the model is called singly
constrained.
2.2 Generalized cost
One of the factors that influences trip distribution is the relative travel cost between two zones. This
cost element may be considered in terms of distance, time or money units. It is often convenient to
use a measure combining all the main attributes related to the dis-utility of a journey
and this is normally referred to as the generalized cost of travel. This can be represented
as
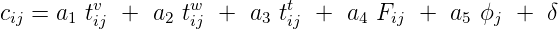 | (1) |
where tijv is the in-vehicle travel time between i and j, t
ijw is the walking time to and from stops, t
ijt
is the waiting time at stops, Fij is the fare charged to travel between i and j, ϕj is the parking cost at
the destination, and δ is a parameter representing comfort and convenience, and a1, a2, .... are the
weights attached to each element of the cost function.
3 Growth factor methods
3.1 Uniform growth factor
If the only information available is about a general growth rate for the whole of the study area, then
we can only assume that it will apply to each cell in the matrix, that is a uniform growth rate. The
equation can be written as:
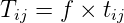 | (2) |
where f is the uniform growth factor tij is the previous total number of trips, Tij is the expanded
total number of trips. Advantages are that they are simple to understand, and they are useful for
short-term planning. Limitation is that the same growth factor is assumed for all zones as well as
attractions.
3.2 Example
Trips originating from zone 1, 2, and 3 of a study area are 78, 92 and 82 respectively and those
terminating at zones 1, 2, and 3 are given as 88, 96 and 78 respectively. If the growth factor is 1.3 and
the base year trip matrix is as given below, find the expanded origin-constrained growth trip
table.
|
|
|
|
|
| | 1 | 2 | 3 | oi |
|
|
|
|
|
| 1 | 20 | 30 | 28 | 78 |
| 2 | 36 | 32 | 24 | 92 |
| 3 | 22 | 34 | 26 | 82 |
|
|
|
|
|
| dj | 88 | 96 | 78 | 252 |
|
|
|
|
|
| |
Solution
Given growth factor = 1.3, Therefore, multiplying the growth factor with each of the cells in the
matrix gives the solution as shown below.
|
|
|
|
|
| | 1 | 2 | 3 | Oi |
|
|
|
|
|
| 1 | 26 | 39 | 36.4 | 101.4 |
| 2 | 46.8 | 41.6 | 31.2 | 119.6 |
| 3 | 28.6 | 44.2 | 33.8 | 106.2 |
|
|
|
|
|
| Dj | 101.4 | 124.8 | 101.4 | 327.6 |
|
|
|
|
|
| |
3.3 Doubly constrained growth factor model
When information is available on the growth in the number of trips originating and terminating in
each zone, we know that there will be different growth rates for trips in and out of each zone and
consequently having two sets of growth factors for each zone. This implies that there are two
constraints for that model and such a model is called doubly constrained growth factor model. One of
the methods of solving such a model is given by Furness who introduced balancing factors ai and bj as
follows:
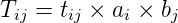 | (3) |
In such cases, a set of intermediate correction coefficients are calculated which are then
appropriately applied to cell entries in each row or column. After applying these corrections to say
each row, totals for each column are calculated and compared with the target values. If the differences
are significant, correction coefficients are calculated and applied as necessary. The procedure is given
below:
- Set bj = 1
- With bj solve for ai to satisfy trip generation constraint.
- With ai solve for bj to satisfy trip attraction constraint.
- Update matrix and check for errors.
- Repeat steps 2 and 3 till convergence.
Here the error is calculated as: E = ∑
|Oi - Oi1| + ∑|D
j - Dj1| where O
i corresponds to the actual
productions from zone i and Oi1 is the calculated productions from that zone. Similarly D
j are
the actual attractions from the zone j and Dj1 are the calculated attractions from that
zone.
3.4 Advantages and limitations of growth factor model
The advantages of this method are:
- Simple to understand.
- Preserve observed trip pattern.
- Useful in short term-planning.
The limitations are:
- Depends heavily on the observed trip pattern.
- It cannot explain unobserved trips.
- Do not consider changes in travel cost.
- Not suitable for policy studies like introduction of a mode.
3.4.1 Example
The base year trip matrix for a study area consisting of three zones is given below.
|
|
|
|
|
| | 1 | 2 | 3 | oi |
|
|
|
|
|
| 1 | 20 | 30 | 28 | 78 |
| 2 | 36 | 32 | 24 | 92 |
| 3 | 22 | 34 | 26 | 82 |
|
|
|
|
|
| dj | 88 | 96 | 78 | 252 |
|
|
|
|
|
| |
The productions from the zone 1,2 and 3 for the horizon year is expected to grow to 98, 106, and 122
respectively. The attractions from these zones are expected to increase to 102, 118, 106 respectively.
Compute the trip matrix for the horizon year using doubly constrained growth factor model using
Furness method.
Solution
The sum of the attractions in the horizon year, i.e. ∑
Oi = 98+106+122 = 326. The sum of the
productions in the horizon year, i.e. ∑
Dj = 102+118+106 = 326. They both are found to be equal.
Therefore we can proceed. The first step is to fix bj = 1, and find balancing factor ai. ai = Oi∕oi, then
find Tij = ai × tij
So a1 = 98∕78 = 1.26
a2 = 106∕92 = 1.15
a3 = 122∕82 = 1.49 Further T11 = t11 ×a1 = 20×1.26 = 25.2. Similarly T12 = t12 ×a2 = 36×1.15 = 41.4.
etc. Multiplying a1 with the first row of the matrix, a2 with the second row and so on, matrix
obtained is as shown below.
|
|
|
|
|
| | 1 | 2 | 3 | oi |
|
|
|
|
|
| 1 | 25.2 | 37.8 | 35.28 | 98 |
| 2 | 41.4 | 36.8 | 27.6 | 106 |
| 3 | 32.78 | 50.66 | 38.74 | 122 |
|
|
|
|
|
| dj1 | 99.38 | 125.26 | 101.62 | |
|
|
|
|
|
| Dj | 102 | 118 | 106 | |
|
|
|
|
|
| |
Also dj1 = 25.2 + 41.4 + 32.78 = 99.38
In the second step, find bj = Dj/dj1 and T
ij = tij × bj. For example b1 = 102∕99.38 = 1.03,
b2 = 118∕125.26 = 0.94 etc.,T11 = t11×b1 = 25.2×1.03 = 25.96 etc. Also Oi1 = 25.96+35.53+36.69 = 98.18.
The matrix is as shown below:
|
|
|
|
|
|
| | 1 | 2 | 3 | oi | Oi |
|
|
|
|
|
|
| 1 | 25.96 | 35.53 | 36.69 | 98.18 | 98 |
| 2 | 42.64 | 34.59 | 28.70 | 105.93 | 106 |
| 3 | 33.76 | 47.62 | 40.29 | 121.67 | 122 |
|
|
|
|
|
|
| bj | 1.03 | 0.94 | 1.04 | | |
|
|
|
|
|
|
| Dj | 102 | 118 | 106 | | |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| | 1 | 2 | 3 | Oi1 | O
i |
|
|
|
|
|
|
| 1 | 25.96 | 35.53 | 36.69 | 98.18 | 98 |
| 2 | 42.64 | 34.59 | 28.70 | 105.93 | 106 |
| 3 | 33.76 | 47.62 | 40.29 | 121.67 | 122 |
|
|
|
|
|
|
| dj | 102.36 | 117.74 | 105.68 | 325.78 | |
|
|
|
|
|
|
| Dj | 102 | 118 | 106 | 326 | |
|
|
|
|
|
|
| |
Therefore error can be computed as ; Error = ∑
|Oi - Oi1| + ∑|D
j - dj|
Error = |98.18-98|+|105.93-106|+|121.67-122|+|102.36-102|+|117.74-118|+|105.68-106| = 1.32
4 Gravity model
This model originally generated from an analogy with Newton’s gravitational law. Newton’s
gravitational law says, F = G M1 M2 ∕ d2 Analogous to this, Tij = C Oi Dj ∕ cijn
Introducing some balancing factors, Tij = Ai Oi Bj Dj f(cij) where Ai and Bj are the balancing
factors, f(cij) is the generalized function of the travel cost. This function is called deterrence function
because it represents the disincentive to travel as distance (time) or cost increases. Some of the
versions of this function are:
The first equation is called the exponential function, second one is called power function where as the
third one is a combination of exponential and power function. The general form of these functions for
different values of their parameters is as shown in figure.
As in the growth factor model, here also we have singly and doubly constrained models. The
expression Tij = Ai Oi Bj Dj f(cij) is the classical version of the doubly constrained model.
Singly constrained versions can be produced by making one set of balancing factors Ai or Bj equal to
one. Therefore we can treat singly constrained model as a special case which can be derived
from doubly constrained models. Hence we will limit our discussion to doubly constrained
models.
As seen earlier, the model has the functional form, Tij = AiOiBjDjf(cij)
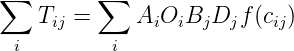 | (4) |
But
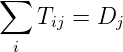 | (5) |
Therefore,
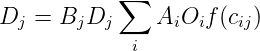 | (6) |
From this we can find the balancing factor Bj as
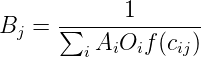 | (7) |
Bj depends on Ai which can be found out by the following equation:
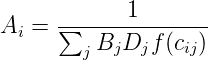 | (8) |
We can see that both Ai and Bj are interdependent. Therefore, through some iteration procedure
similar to that of Furness method, the problem can be solved. The procedure is discussed
below:
- Set Bj = 1, find Ai using equation 8
- Find Bj using equation 7
- Compute the error as E = ∑
|Oi - Oi1| + ∑|D
j - Dj1| where O
i corresponds to the
actual productions from zone i and Oi1 is the calculated productions from that zone.
Similarly Dj are the actual attractions from the zone j and Dj1 are the calculated
attractions from that zone.
- Again set Bj = 1 and find Ai, also find Bj. Repeat these steps until the convergence is
achieved.
4.0.1 Example
The productions from zone 1, 2 and 3 are 98, 106, 122 and attractions to zone 1,2 and 3 are 102,
118, 106. The function f(cij) is defined as f(cij) = 1∕cij2 The cost matrix is as shown
below
 | (9) |
Solution
The first step is given in Table 1
Table 1: Step1: Computation of parameter Ai
|
|
|
|
|
|
|
|
| i | j | Bj | DJ | f(cij) | BjDjf(cij) | ∑
BjDjf(cij) | Ai = 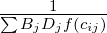 |
|
|
|
|
|
|
|
|
| | 1 | 1.0 | 102 | 1.0 | 102.00 | | |
| 1 | 2 | 1.0 | 118 | 0.69 | 81.42 | 216.28 | 0.00462 |
| | 3 | 1.0 | 106 | 0.31 | 32.86 | | |
|
|
|
|
|
|
|
|
| | 1 | 1.0 | 102 | 0.69 | 70.38 | | |
| 2 | 2 | 1.0 | 118 | 1.0 | 118 | 235.02 | 0.00425 |
| | 3 | 1.0 | 106 | 0.44 | 46.64 | | |
|
|
|
|
|
|
|
|
| | 1 | 1.0 | 102 | 0.31 | 31.62 | | |
| 3 | 2 | 1.0 | 118 | 0.44 | 51.92 | 189.54 | 0.00527 |
| | 3 | 1.0 | 106 | 1.00 | 106 | | |
|
|
|
|
|
|
|
|
| |
The second step is to find Bj. This can be found out as Bj = 1∕∑
AiOif(cij), where Ai is
obtained from the previous step. The detailed computation is given in Table 2.
Table 2: Step2: Computation of parameter Bj
|
|
|
|
|
|
|
|
| j | i | Ai | Oi | f(cij) | AiOif(cij) | ∑
AiOif(cij) | Bj = 1∕∑
AiOif(cij) |
|
|
|
|
|
|
|
|
| | 1 | 0.00462 | 98 | 1.0 | 0.4523 | | |
| 1 | 2 | 0.00425 | 106 | 0.694 | 0.3117 | 0.9618 | 1.0397 |
| | 3 | 0.00527 | 122 | 0.308 | 0.1978 | | |
|
|
|
|
|
|
|
|
| | 1 | 0.00462 | 98 | 0.69 | 0.3124 | | |
| 2 | 2 | 0.00425 | 106 | 1.0 | 0.4505 | 1.0458 | 0.9562 |
| | 3 | 0.00527 | 122 | 0.44 | 0.2829 | | |
|
|
|
|
|
|
|
|
| | 1 | 0.00462 | 98 | 0.31 | 0.1404 | | |
| 3 | 2 | 0.00425 | 106 | 0.44 | 0.1982 | 0.9815 | 1.0188 |
| | 3 | 0.00527 | 122 | 1.00 | 0.6429 | | |
|
|
|
|
|
|
|
|
| |
The function f(cij) can be written in the matrix form as:
 | (10) |
Then Tij can be computed using the formula
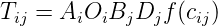 | (11) |
For eg, T11 = 102 × 1.0397 × 0.00462 × 98 × 1 = 48.01. Oi is the actual productions from the zone and
Oi1 is the computed ones. Similar is the case with attractions also. The results are shown in
table 3.
Table 3: Step3: Final Table
|
|
|
|
|
|
|
| | 1 | 2 | 3 | Ai | Oi | Oi1 |
|
|
|
|
|
|
|
| 1 | 48.01 | 35.24 | 15.157 | 0.00462 | 98 | 98.407 |
|
|
|
|
|
|
|
| 2 | 32.96 | 50.83 | 21.40 | 0.00425 | 106 | 105.19 |
|
|
|
|
|
|
|
| 3 | 21.14 | 31.919 | 69.43 | 0.00527 | 122 | 122.489 |
|
|
|
|
|
|
|
| Bj | 1.0397 | 0.9562 | 1.0188 | | | |
|
|
|
|
|
|
|
| Dj | 102 | 118 | 106 | | | |
|
|
|
|
|
|
|
| Dj1 | 102.11 | 117.989 | 105.987 | | | |
|
|
|
|
|
|
|
| |
Oi is the actual productions from the zone and Oi1 is the computed ones. Similar is the case with
attractions also.
Therefore error can be computed as ; Error = ∑
|Oi - Oi1| + ∑|D
j - Dj1|
Error = |98-98.407|+|106-105.19|+|122-122.489|+||102-102.11|+|118-117.989|+|106-105.987| = 2.03
5 Summary
The second stage of travel demand modeling is the trip distribution. Trip matrix can be used to
represent the trip pattern of a study area. Growth factor methods and gravity model are
used for computing the trip matrix. Singly constrained models and doubly constrained
growth factor models are discussed. In gravity model, considering singly constrained model
as a special case of doubly constrained model, doubly constrained model is explained in
detail.
6 Problems
The trip productions from zones 1, 2 and 3 are 110, 122 and 114 respectively and the trip attractions
to these zones are 120,108, and 118 respectively. The cost matrix is given below. The function
f(cij) = 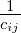
Compute the trip matrix using doubly constrained gravity model. Provide one complete
iteration.
Solution
The first step is given in Table 4
Table 4: Step1: Computation of parameter Ai
|
|
|
|
|
|
|
|
| i | j | Bj | DJ | f(cij) | BjDjf(cij) | ∑
BjDjf(cij) | Ai = 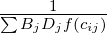 |
|
|
|
|
|
|
|
|
| | 1 | 1.0 | 120 | 1.0 | 120.00 | | |
| 1 | 2 | 1.0 | 108 | 0.833 | 89.964 | 275.454 | 0.00363 |
| | 3 | 1.0 | 118 | 0.555 | 65.49 | | |
|
|
|
|
|
|
|
|
| | 1 | 1.0 | 120 | 0.833 | 99.96 | | |
| 2 | 2 | 1.0 | 108 | 1.0 | 108 | 286.66 | 0.00348 |
| | 3 | 1.0 | 118 | 0.667 | 78.706 | | |
|
|
|
|
|
|
|
|
| | 1 | 1.0 | 120 | 0.555 | 66.60 | | |
| 3 | 2 | 1.0 | 108 | 0.667 | 72.036 | 256.636 | 0.00389 |
| | 3 | 1.0 | 118 | 1.00 | 118 | | |
|
|
|
|
|
|
|
|
| |
The second step is to find Bj. This can be found out as Bj = 1∕∑
AiOif(cij), where Ai is
obtained from the previous step.
Table 5: Step2: Computation of parameter Bj
|
|
|
|
|
|
|
|
| j | i | Ai | Oi | f(cij) | AiOif(cij) | ∑
AiOif(cij) | Bj = 1∕∑
AiOif(cij) |
|
|
|
|
|
|
|
|
| | 1 | 0.00363 | 110 | 1.0 | 0.3993 | | |
| 1 | 2 | 0.00348 | 122 | 0.833 | 0.3536 | 0.9994 | 1.048 |
| | 3 | 0.00389 | 114 | 0.555 | 0.2465 | | |
|
|
|
|
|
|
|
|
| | 1 | 0.00363 | 110 | 0.833 | 0.3326 | | |
| 2 | 2 | 0.00348 | 122 | 1.0 | 0.4245 | 1.05 | 0.9494 |
| | 3 | 0.00389 | 114 | 0.667 | 0.2962 | | |
|
|
|
|
|
|
|
|
| | 1 | 0.00363 | 110 | 0555 | 0.2216 | | |
| 3 | 2 | 0.00348 | 122 | 0.667 | 0.2832 | 0.9483 | 1.054 |
| | 3 | 0.00389 | 114 | 1.00 | 0.44346 | | |
|
|
|
|
|
|
|
|
| |
The function f(cij) can be written in the matrix form as:
 | (12) |
Then Tij can be computed using the formula
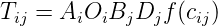 | (13) |
For eg, T11 = 102 × 1.0397 × 0.00462 × 98 × 1 = 48.01. Oi is the actual productions from the zone and
Oi1 is the computed ones. Similar is the case with attractions also. This step is given in Table
6
Table 6: Step 3: Final Table
|
|
|
|
|
|
|
| | 1 | 2 | 3 | Ai | Oi | Oi1 |
|
|
|
|
|
|
|
| 1 | 48.01 | 34.10 | 27.56 | 0.00363 | 110 | 109.57 |
|
|
|
|
|
|
|
| 2 | 42.43 | 43.53 | 35.21 | 0.00348 | 122 | 121.17 |
|
|
|
|
|
|
|
| 3 | 29.53 | 30.32 | 55.15 | 0.00389 | 114 | 115 |
|
|
|
|
|
|
|
| Bj | 1.048 | 0.9494 | 1.054 | | | |
|
|
|
|
|
|
|
| Dj | 120 | 108 | 118 | | | |
|
|
|
|
|
|
|
| Dj1 | 119.876 | 107.95 | 117.92 | | | |
|
|
|
|
|
|
|
| |
Oi is the actual productions from the zone and Oi1 is the computed ones. Similar is the case with
attractions also.
Therefore error can be computed as ; Error = ∑
|Oi - Oi1| + ∑|D
j - Dj1|
Error = |110-109.57|+|122-121.17|+|114-115|+|120-119.876+|108-107.95|+|118-117.92| = 2.515
Exercises
- Not Available
References
- J D Ortuzar and L G Willumnsen. Modeling Transport. John Wiley and Sons, New
York, 1994.
Acknowledgments
I wish to thank several of my students and staff of NPTEL for their contribution in this lecture. I
also appreciate your constructive feedback which may be sent to tvm@civil.iitb.ac.in
Prof. Tom V. Mathew
Department of Civil Engineering
Indian Institute of Technology Bombay, India
____________________________________________________________________________________________
Thu Jan 10 12:40:59 IST 2019