Marshall Mix Design

Lecture Notes in Transportation Systems Engineering

Prof. Tom V. Mathew

Contents

1 Overview
2 Marshall mix design
3 Specimen preparation
4 Properties of the mix
 4.1 Theoretical specific gravity of the mix Gt
 4.2 Bulk specific gravity of mix Gm
 4.3 Air voids percent V v
 4.4 Percent volume of bitumen V b
 4.5 Voids in mineral aggregateV MA
 4.6 Voids filled with bitumen V FB
5 Determine Marshall stability and flow
6 Apply stability correction
7 Prepare graphical plots
8 Determine optimum bitumen content
9 Numerical example - 1
10 Numerical example - 2
11 Summary
12 Problems
13 Solutions
Exercises
References
Acknowledgments
_________________________________________________________________________________________

1 Overview

The mix design (wetmix) determines the optimum bitumen content. This is preceded by the dry mix design discussed in the previous chapter. There are many methods available for mix design which vary in the size of the test specimen, compaction, and other test specifications. Marshall method of mix design is the most popular one and is discussed below.

2 Marshall mix design

The Marshall stability and flow test provides the performance prediction measure for the Marshall mix design method. The stability portion of the test measures the maximum load supported by the test specimen at a loading rate of 50.8 mm/minute. Load is applied to the specimen till failure, and the maximum load is designated as stability. During the loading, an attached dial gauge measures the specimen’s plastic flow (deformation) due to the loading. The flow value is recorded in 0.25 mm (0.01 inch) increments at the same time when the maximum load is recorded. The important steps involved in marshal mix design are summarized next.

3 Specimen preparation

Approximately 1200gm of aggregates and filler is heated to a temperature of 175 - 190oC. Bitumen is heated to a temperature of 121 - 125oC with the first trial percentage of bitumen (say 3.5 or 4% by weight of the mineral aggregates). The heated aggregates and bitumen are thoroughly mixed at a temperature of 154 - 160oC. The mix is placed in a preheated mould and compacted by a rammer with 50 blows on either side at temperature of 138oC to 149oC. The weight of mixed aggregates taken for the preparation of the specimen may be suitably altered to obtain a compacted thickness of 63.5+/-3 mm. Vary the bitumen content in the next trial by +0.5% and repeat the above procedure. Number of trials are predetermined. The prepared mould is loaded in the Marshall test setup as shown in the figure 1.

PIC

Figure 1: Marshall test setup

4 Properties of the mix

The properties that are of interest include the theoretical specific gravity Gt, the bulk specific gravity of the mix Gm, percent air voids V v, percent volume of bitumen V b, percent void in mixed aggregate VMA and percent voids filled with bitumen VFB. These calculations are discussed next. To understand these calculation a phase diagram is given in Figure 2.

PIC

Figure 2: Phase diagram of a bituminous mix

4.1 Theoretical specific gravity of the mix Gt

Theoretical specific gravity Gt is the specific gravity without considering air voids, and is given by:

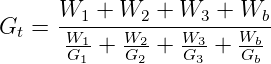W + W + W + W Gt = W-1---W2---W-3---W-b- G11+ G22-+ G33+ Gbb-
(1)

where, W1 is the weight of coarse aggregate in the total mix, W2 is the weight of fine aggregate in the total mix, W3 is the weight of filler in the total mix, Wb is the weight of bitumen in the total mix, G1 is the apparent specific gravity of coarse aggregate, G2 is the apparent specific gravity of fine aggregate, G3 is the apparent specific gravity of filler and Gb is the apparent specific gravity of bitumen,

4.2 Bulk specific gravity of mix Gm

The bulk specific gravity or the actual specific gravity of the mix Gm is the specific gravity considering air voids and is found out by:

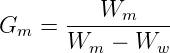G = ---Wm----- m Wm - Ww
(2)

where, Wm is the weight of mix in air, Ww is the weight of mix in water, Note that Wm - Ww gives the volume of the mix. Sometimes to get accurate bulk specific gravity, the specimen is coated with thin film of paraffin wax, when weight is taken in the water. This, however requires to consider the weight and volume of wax in the calculations.

4.3 Air voids percent V v

Air voids V v is the percent of air voids by volume in the specimen and is given by:

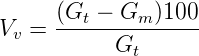V = (Gt---Gm-)100- v Gt
(3)

where Gt is the theoretical specific gravity of the mix, given by equation 26.1. and Gm is the bulk or actual specific gravity of the mix given by equation 26.2.

4.4 Percent volume of bitumen V b

The volume of bitumen V b is the percent of volume of bitumen to the total volume and given by:

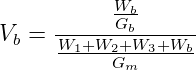WGb- Vb = W1+W2+Wb3+Wb--- -----Gm------
(4)

where, W1 is the weight of coarse aggregate in the total mix, W2 is the weight of fine aggregate in the total mix, W3 is the weight of filler in the total mix, Wb is the weight of bitumen in the total mix, Gb is the apparent specific gravity of bitumen, and Gm is the bulk specific gravity of mix given by equation 26.2.

4.5 Voids in mineral aggregateV MA

Voids in mineral aggregate V MA is the volume of voids in the aggregates, and is the sum of air voids and volume of bitumen, and is calculated from

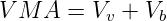V M A = Vv + Vb
(5)

where, V v is the percent air voids in the mix, given by equation 26.3. and V b is percent bitumen content in the mix, given by equation 26.4.  (4).

4.6 Voids filled with bitumen V FB

Voids filled with bitumen V FB is the voids in the mineral aggregate frame work filled with the bitumen, and is calculated as:

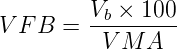V F B = Vb-×-100- V M A
(6)

where, V b is percent bitumen content in the mix, given by equation 26.4. and V MA is the percent voids in the mineral aggregate, given by equation 26.5.

5 Determine Marshall stability and flow

Marshall stability of a test specimen is the maximum load required to produce failure when the specimen is preheated to a prescribed temperature placed in a special test head and the load is applied at a constant strain (5 cm per minute). While the stability test is in progress dial gauge is used to measure the vertical deformation of the specimen. The deformation at the failure point expressed in units of 0.25 mm is called the Marshall flow value of the specimen.

6 Apply stability correction

It is possible while making the specimen the thickness slightly vary from the standard specification of 63.5 mm. Therefore, measured stability values need to be corrected to those which would have been obtained if the specimens had been exactly 63.5 mm. This is done by multiplying each measured stability value by an appropriated correlation factors as given in Table below.


Table 1: Correction factors for Marshall stability values
Volume of Thickness Correction
specimen of specimen Factor
(cm3) (mm)
457 - 470 57.1 1.19
471 - 482 68.7 1.14
483 - 495 60.3 1.09
496 - 508 61.9 1.04
509 - 522 63.5 1.00
523 - 535 65.1 0.96
536 - 546 66.7 0.93
547 - 559 68.3 0.89
560 - 573 69.9 0.86

7 Prepare graphical plots

The average value of the above properties are determined for each mix with different bitumen content and the following graphical plots are prepared:

  1. Binder content versus corrected Marshall stability
  2. Binder content versus Marshall flow
  3. Binder content versus percentage of void (V v) in the total mix
  4. Binder content versus voids filled with bitumen (V FB)
  5. Binder content versus unit weight or bulk specific gravity (Gm)

8 Determine optimum bitumen content

Determine the optimum binder content for the mix design by taking average value of the following three bitumen contents found form the graphs obtained in the previous step.

  1. Binder content corresponding to maximum stability
  2. Binder content corresponding to maximum bulk specific gravity (Gm)
  3. Binder content corresponding to the median of designed limits of percent air voids (V v) in the total mix (i.e. 4%)

The stability value, flow value, and V FB are checked with Marshall mix design specification chart given in Table below. Mixes with very high stability value and low flow value are not desirable as the pavements constructed with such mixes are likely to develop cracks due to heavy moving loads.


Table 2: Marshall mix design specification
Test Property Specified Value
Marshall stability, kg 340 (minimum)
Flow value, 0.25 mm units 8 - 17
Percent air voids in the mix V v% 3 - 5
Voids filled with bitumen V FB% 75 - 85


Figure 3: Marshal graphical plots

9 Numerical example - 1

The specific gravities and weight proportions for aggregate and bitumen are as under for the preparation of Marshall mix design. The volume and weight of one Marshall specimen was found to be 475 cc and 1100 gm. Assuming absorption of bitumen in aggregate is zero, find V v, V b, V MA and V FB;

Item A_1 A_2 A_3 A_4 B
Wt (gm) 825 1200 325 150 100
Sp. Gr 2.63 2.51 2.46 2.43 1.05

Solution

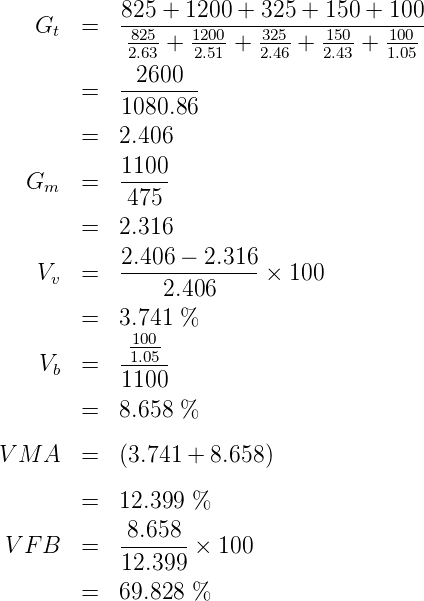
G = 825-+-1200-+--325 +-150-+-100 t 822.653 + 122.5001-+ 232.546 + 21.5043 + 11.0005 2600 = -------- 1080.86 = 2.406 1100 Gm = ----- 475 = 2.316 2.406---2.316 Vv = 2.406 × 100 = 3.170401 % -1.05- Vb = 1100 = 8.658 % VM A = (3.741 + 8.658 ) = 12.399 % 8.658 V F B = -------× 100 12.399 = 69.828 %

10 Numerical example - 2

The results of Marshall test for five specimen is given below. Find the optimum bitumen content of the mix.

Bitumen Stability Flow V v V FB Gm
content (kg) (units) (%) (%)
3 499.4 9.0 12.5 34 2.17
4 717.3 9.6 7.2 65 2.21
5 812.7 12.0 3.9 84 2.26
6 767.3 14.8 2.4 91 2.23
7 662.8 19.5 1.9 93 2.18

Solution Plot the graphs and find bitumen content corresponding to

  1. Max stability = 5 percent bitumen content.
  2. Max Gm = 5 percent bitumen content.
  3. 4% percent air void = 3 percent bitumen content.

The optimum bitumen extent is the average of above = 4.33 percent.

11 Summary

Marshal stability test is the performance prediction measure conducted on the bituminous nix. The procedure consists of determination of properties of mix, Marshal stability and flow analysis and finally determination of optimum bitumen content. The concept of phase diagram is used for the calculations.

12 Problems

  1. In Marshall stability test, the sample is compacted using a rammer giving
    1. 50 blows
    2. 20 blows
    3. 25 blows
    4. 75 blows
  2. The Marshall flow value is expressed in units of
    1. 25 mm
    2. 2.5mm
    3. 5mm
    4. 3mm

13 Solutions

  1. In Marshall stability test, the sample is compacted using a rammer giving
    1. 50 blows√
    2. 20 blows
    3. 25 blows
    4. 75 blows
  2. The Marshall flow value is expressed in units of
    1. 25 mm
    2. 2.5mm√
    3. 5mm
    4. 3mm

Exercises

  1. Not Available

References

  1. Y. H Huang. Pavement analysis and Design. Prentice-Hall, Englewood Cliffs, New Jersey, 1993.

Acknowledgments

I wish to thank several of my students and staff of NPTEL for their contribution in this lecture. I also appreciate your constructive feedback which may be sent to tvm@civil.iitb.ac.in

Prof. Tom V. Mathew
Department of Civil Engineering
Indian Institute of Technology Bombay, India

____________________________________________________________________________________________

Fri May 24 16:23:19 IST 2019