
For a complete description of traffic stream modeling, one would require flow, speed, and density. Obtaining these parameters simultaneously is a difficult task if we use separate techniques. Since we have a fundamental equation of traffic flow, which gives the flow as the product of density and space mean speed, if we knew any two parameters, the third can be computed. Moving car or moving observer method of traffic stream measurement has been developed to provide simultaneous measurement of traffic stream variables. It has the advantage of obtaining the complete state with just three observers, and a vehicle. Determination of any of the two parameters of the traffic flow will provide the third one by the equation q = u.k. Thus, moving observer method is the most commonly used method to get the relationship between the fundamental stream characteristics. In this method, the observer moves in the traffic stream unlike all other previous methods.
Consider a stream of vehicles moving in the north bound direction. Two different cases of motion can be considered. The first case considers the traffic stream to be moving and the observer to be stationary.
If no is the number of vehicles overtaking the observer during a period, t, then flow q is 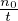 ,
or
,
or
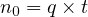 | (1) |
The second case assumes that the stream is stationary and the observer moves with speed
vo. If np is the number of vehicles overtaken by observer over a length l, then by definition,
density k is 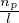 , or
, or
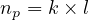 | (2) |
or
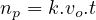 | (3) |
where v0 is the speed of the observer and t is the time taken for the observer to cover the road stretch. Now consider the case when the observer is moving within the stream. In that case mo vehicles will overtake the observer and mp vehicles will be overtaken by the observer in the test vehicle. Let the difference m is given by m0 - mp, then from equation 1 and equation 3,
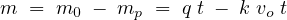 | (4) |
This equation is the basic equation of moving observer method, which relates q,k to the counts m, t and vo that can be obtained from the test. However, we have two unknowns, q and k, but only one equation. For generating another equation, the test vehicle is run twice once with the traffic stream and another one against traffic stream, i.e.
where, a,w denotes against and with traffic flow. It may be noted that the sign of equation 6 is negative, because test vehicle moving in the opposite direction can be considered as a case when the test vehicle is moving in the stream with negative velocity. Further, in this case, all the vehicles will be overtaking, since it is moving with negative speed. In other words, when the test vehicle moves in the opposite direction, the observer simply counts the number of vehicles in the opposite direction. Adding equation 5 and 6, we will get the first parameter of the stream, namely the flow(q) as:
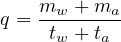 | (7) |
Now calculating space mean speed from equation 5,
![mw- = q- kvw
tw
= q- qvw
v [ ]
= q- q l-
v tw
( l -1 )
= q 1 - v × tw
( t )
= q 1 - avg-
tw](web8x.png)
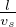 . Therefore,
. Therefore,
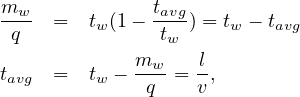
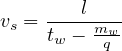 | (8) |
Thus two parameters of the stream can be determined. Knowing the two parameters the third parameter of traffic flow density (k) can be found out as
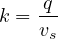 | (9) |
For increase accuracy and reliability, the test is performed a number of times and the average results are to be taken.
The length of a road stretch used for conducting the moving observer test is 0.5 km and the speed with which the test vehicle moved is 20 km/hr. Given that the number of vehicles encountered in the stream while the test vehicle was moving against the traffic stream is 107, number of vehicles that had overtaken the test vehicle is 10, and the number of vehicles overtaken by the test vehicle is 74, find the flow, density and average speed of the stream.
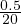 = 0.025 hr
= 0.025 hr
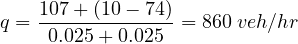 |
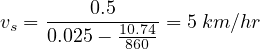 |
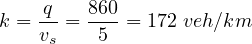 |
| No | ma | mo | mp | mw = (mo - mp) | ta | tw | q = 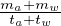 | u = 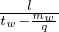 | k = 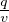 |
| 1 | 107 | 10 | 74 | -64 | 0.025 | 0.025 | 860 | 5.03 | 171 |
| 2 | 113 | 25 | 41 | -16 | 0.025 | 0.025 | 1940 | 15.04 | 129 |
| 3 | 30 | 15 | 5 | 10 | 0.025 | 0.025 | 800 | 40 | 20 |
| 4 | 79 | 18 | 9 | 9 | 0.025 | 0.025 | 1760 | 25.14 | 70 |
The data from four moving observer test methods are shown in the table. Column 1 gives the sample number, column 2 gives the number of vehicles moving against the stream, column 3 gives the number of vehicles that had overtaken the test vehicle, and last column gives the number of vehicles overtaken by the test vehicle. Find the three fundamental stream parameters for each set of data. Also plot the fundamental diagrams of traffic flow.
| No | 1 | 2 | 3 |
| 1 | 107 | 10 | 74 |
| 2 | 113 | 25 | 41 |
| 3 | 30 | 15 | 5 |
| 4 | 79 | 18 | 9 |
Solution From the calculated values of flow, density and speed, the three fundamental diagrams can be plotted as shown in figure 2.
Traffic engineering studies differ from other studies in the fact that they require extensive data from the field which cannot be exactly created in any laboratory. Speed data are collected from measurements at a point or over a short section or over an area. Traffic flow data are collected at a point. Moving observer method is one in which both speed and traffic flow data are obtained by a single experiment.
| (1) | (2) | (3) | (4) | (5) |
| 5 | 119 | 618 | 422 | 268 |
| 26 | 12 | 389 | 213 | 188 |
| 24 | 9 | 401 | 226 | 396 |
| 2 | 55 | 410 | 274 | 255 |
| 26 | 9 | 374 | 226 | 396 |
I wish to thank several of my students and staff of NPTEL for their contribution in this lecture. I also appreciate your constructive feedback which may be sent to tvm@civil.iitb.ac.in
Prof. Tom V. Mathew
Department of Civil Engineering
Indian Institute of Technology Bombay, India
_________________________________________________________________________
Monday 21 August 2023 12:19:24 AM IST