The main purpose of this chapter is to determine traffic parameter, specially speed. Speed measurements are most often taken at a point (or a short section) of road way under conditions of free flow. The intent is to determine the speeds that drivers select, unaffected by the existence of congestion. This information is used to determine general speed trends, to help determine reasonable speed limits, and to assess safety.
As speed defines the distance travelled by user in a given time, and this is a vibrant in every traffic movement. In other words speed of movement is the ratio of distance travelled to time of travel. The actual speed of traffic flow over a given route may fluctuated widely, as because at each time the volume of traffic varies. Accordingly, speeds are generally classified into three main categories
When we measure the traffic parameter over a short distance, we generally measure the spot speed. A spot speed is made by measuring the individual speeds of a sample of the vehicle passing a given spot on a street or highway. Spot speed studies are used to determine the speed distribution of a traffic stream at a specific location. The data gathered in spot speed studies are used to determine vehicle speed percentiles, which are useful in making many speed-related decisions. Spot speed data have a number of safety applications, including the following
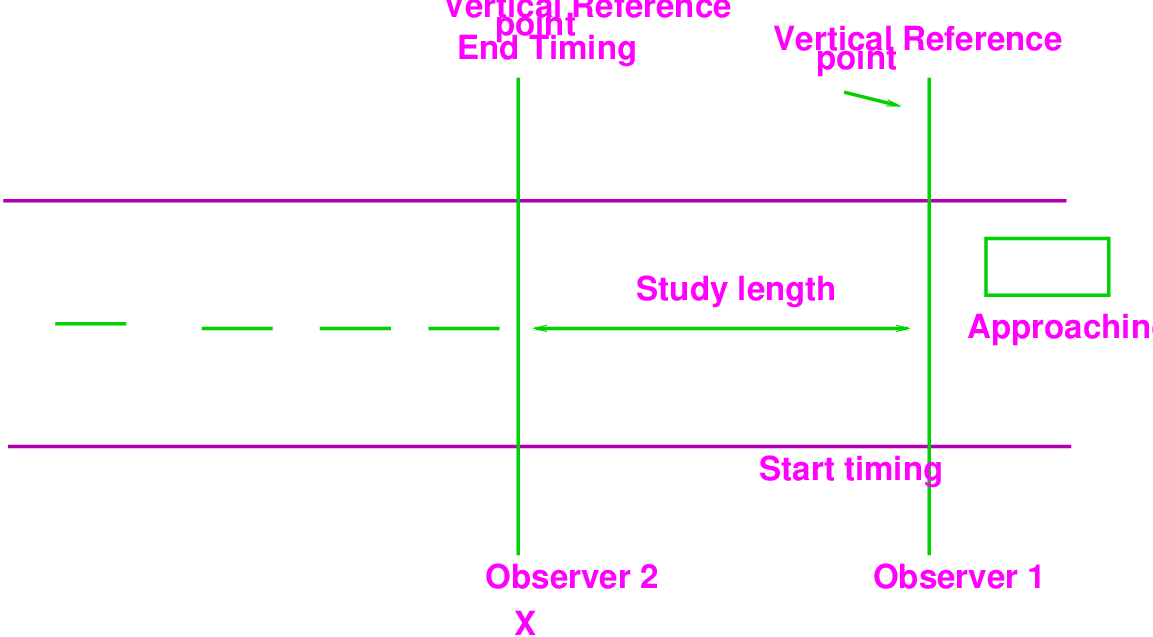
Methods of conducting spot speed Studies are divided into two main categories: Manual and Automatic. Spot speeds may be estimated by manually measuring the time it takes a vehicle to travel between two defined points on the roadway a known distance apart (short distance), usually less than 90m. Distance between two points is generally depending upon the average speed of traffic stream. Following tables gives recommended study length (in meters) for various average stream speed ranges (in kmph)
| Stream Speed | Length |
| below 15 | 30 |
| 15 -25 | 60 |
| above 25 | 90 |
Following are the some methods to measure spot speed of vehicles in a traffic stream, in which first two are manual methods and other are automatic:
In this method, markings of pavement are placed across the road at each end of trap. Observer start and stops the watch as vehicle passes lines. In this method, minimum two observers required to collect the data, of which one is stand at the starting point to start and stop the stop watch and other one is stand at end point to give indication to stop the watch when vehicle passes the end line. Advantages of this method are that after the initial installation no set-up time is required, markings are easily renewed, and disadvantage of this is that substantial error can be introduced, and magnitude of error may change for substitute studies and this method is only applicable for low traffic conditions.
Enoscope consists of a simple open housing containing a mirror mounted on a tripod at the side of the road in such a way that an observer’s line of sight turned through 90o. The observer stands at one end of section and on the other end enoscope is placed and measure the time taken by the vehicle to cross the section (fig 6.2). Advantages of this method are that it simple and eliminate the errors due to parallax and considerable time is required to time each vehicle, which lengthen the study period and under heavy traffic condition it may be difficult to relate ostentatious to proper vehicle are the disadvantages of enoscope method.
Pressure contact strips, either pneumatic or electric, can be used to avoid error due to parallax and due to manually starting and stopping the chronometer or stopwatch. This is the best method over short distance it gives quite relevant data and if it is connected through graphical recorder then it gives continuous data automatically.
This is recently developed method, it automatically records speed, employs a radar transmitter-receiver unit. The apparatus transmits high frequency electromagnetic waves in a narrow beam towards the moving vehicle, and reflected waves changed their length depending up on the vehicles speed and returned to the receiving unit, through calibration gives directly spot speed of the vehicle.
In this method a camera records the distance moved by a vehicle in a selected short time. In this exposure of photograph should be in a constant time interval and the distance travelled by the vehicle is measured by projecting the films during the exposure interval. The main advantage of method that, it gives a permanent record with 100% sample obtained. This method is quite expensive and generally used in developed cities. In this we can use video recorder which give more accurate result.
The measured data by the above techniques should be collected into some formats, following are the some types of data collection sheets which are used for manual and automatic methods,
From the above methods, the collected data have to present into the some representable form, this makes its calculation and analysis simpler and easier. The following methods to present the spot speed data:
After the collection of data in the given conditions, arrange the spot speed values in order to their magnitudes. Then select an interval speed (e.g. 5 kmph) and make grouping of data which come under this range. Now, prepare the frequency distribution table.
For each speed group, the % frequency of observations within the group is plotted versus the middle (mid-mark) speed of the group(s). As shown in Fig 6.5. From this curve the modal speed and pace of traffic flow can be determine. Generally the shape of the curve follows the normal distribution curve, this because the most of the vehicles move on road near by mean speed and very few deviate from mean speed.
For each speed group, the % cumulative frequency of observations is plotted versus the higher limit of the speed group (Fig 6.5). The cumulative frequency distribution curve, however, results in a very useful plot of speed versus the percent of vehicles traveling at or below the designated speed. For this reason, the upper limit of the speed group is used as the plotting point. In both the distribution curve, the plots are connected by a smooth curve that minimizes the total distance of points falling above the line and those falling below the line. A smooth curve is defined as one without.
Common descriptive statistics may be computed from the data in the frequency distribution table or determined graphically from the frequency and cumulative frequency distribution curves. These statistics are used to describe two important characteristics of the distribution:
Measure which helps to describe the approximate middle or center of the distribution. Measures of central tendency include the average or mean speed, the median speed, the modal speed, and the pace.
The arithmetic (or harmonic) average speed is the most frequently used speed statistics. It is the measure of central tendency of the data. Mean calculated gives two kinds of mean speeds.
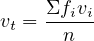 | (1) |
where, vt is the mean or average speed, vi is the individual speed of the ith vehicle, fi is the frequency of speed, and n is the total no of vehicle observed (sample size). Time mean Speed If data collected at a point over a period of time, e.g. by radar meter or stopwatch, produce speed distribution over time, so the mean of speed is time mean speed. Space mean Speed If data obtained over a stretch (section) of road almost instantaneously, aerial photography or enoscope, result in speed distribution in space and mean is space mean speed. Distribution over space and time are not same. Time mean speed is higher than the space mean speed. The spot speed sample at one end taken over a finite period of time will tend to include some fast vehicles which had not yet entered the section at the start of the survey, but will exclude some of the slower vehicles. The relationship between the two mean speeds is expressed by:
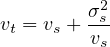 | (2) |
where, vt and vs are the time mean speed and space mean speed respectively. And σs is the standard deviation of distribution space.
The median speed is defined as the speed that divides the distribution in to equal parts (i.e., there are as many observations of speeds higher than the median as there are lower than the median). It is a positional value and is not affected by the absolute value of extreme observations. By definition, the median equally divides the distribution. Therefore, 50% of all observed speeds should be less than the median. In the cumulative frequency curve, the 50th percentile speed is the median of the speed distribution. Median Speed = v50
The pace is a traffic engineering measure not commonly used for other statistical analyses. It is defined as the 10Km/h increment in speed in which the highest percentage of drivers is observed. It is also found graphically using the frequency distribution curve. As shown in fig 6.5. The pace is found as follows: A 10 Km/h template is scaled from the horizontal axis. Keeping this template horizontal, place an end on the lower left side of the curve and move slowly along the curve. When the right side of the template intersects the right side of the curve, the pace has been located. This procedure identifies the 10 Km/h increments that intersect the peak of the curve; this contains the most area and, therefore, the highest percentage of vehicles.
The mode is defined as the single value of speed that is most likely to occur. As no discrete values were recorded, the modal speed is also determined graphically from the frequency distribution curve. A vertical line is dropped from the peak of the curve, with the result found on the horizontal axis.
Measures describe the extent to which data spreads around the center of the distribution. Measures of dispersion include the different percentile speeds i.e. 15th, 85th,etc. and the standard deviation.
The most common statistical measure of dispersion in a distribution is the standard deviation. It is a measure of how far data spreads around the mean value. In simple terms, the standard deviation is the average value of the difference between individual observations and the average value of those observations. The Standard deviation, σs, of the sample can be calculated by
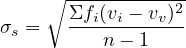 | (3) |
The 85th and 15th percentile speeds give a general description of the high and low speeds observed by most reasonable drivers. It is generally thought that the upper and lower 15% of the distribution represents speeds that are either too fast or too slow for existing conditions. These values are found graphically from the cumulative frequency distribution curve of Figure 6.4. The curve is entered on the vertical axis at values of 85% and 15%. The respective speeds are found on the horizontal axis. The 85th and 15th percentile speeds can be used to roughly estimate the standard deviation of the distribution σest, although this is not recommended when the data is available for a precise determination.
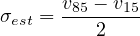 | (4) |
The 85th and 15th percentile speeds give insight to both the central tendency and dispersion of the distribution. As these values get closer to the mean, less dispersion exists and the stronger the central tendency of the distribution becomes.
The 98th percentile speed is also determining from the cumulative frequency curve, this speed is generally used for geometric design of the road.
The means of different sample taken from the same population are distributed normally about the true mean of population with a standard deviation, is known as standard error.
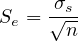 | (5) |
Generally, sample sizes of 50 to 200 vehicles are taken. In that case, standard error of mean is usually under the acceptable limit. If precision is prior then minimum no. of sample should be taken, that can be measured by using the following equation.
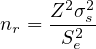 | (6) |
where, nr is the no. of sample required, σs is the Standard deviation, Z is value calculated from Standard Normal distribution Table for a particular confidence level (i.e. for 95% confidence Z=1.96 and for 99.7% confidence Z=3.0) and Se is the permissible (acceptable) error in mean calculation.
Confidence intervals express the range within which a result for the whole population would occur for a particular proportion of times an experiment or test was repeated among a sample of the population. Confidence interval is a standard way of articulate the statistical accuracy of an experiment based assessment. If assess has a high error level, the equivalent confidence interval will be ample, and the less confidence we can have that the experiment results depict the situation among the whole population. When quoting confidence It is common to refer to the some confidence interval around an experiment assessment or test result. So, the confidence interval for estimated true mean speed can be calculated by
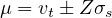 | (7) |
where, μ is the confidence interval, vt is mean speed, σs is standard deviation and Z is constant for specified confidence.
Using the spot speed data given in the following table, collected from a freeway site operating under free-flow conditions: (i) Plot the frequency and cumulative frequency curves for these data; (ii) Obtain median speed, modal speed, pace, and percent vehicles in pace from these plots; (iii) Compute the mean and standard deviation of the speed distribution; (iv) The confidence bounds on the estimate of the true mean speed of the underlying distribution with 95% confidence? With 99.7% confidence; and (v) Based on these results, compute the sample size needed to achieve a tolerance of ±1.5 kmph with 95% confidence.
| Speed Range | Frequency fi |
| 21-25 | 2 |
| 26-30 | 6 |
| 31-35 | 18 |
| 36-40 | 25 |
| 41-45 | 19 |
| 46-50 | 16 |
| 51-55 | 17 |
| 56-60 | 12 |
| 61-65 | 7 |
| 66-70 | 4 |
| 71-75 | 3 |
| 76-80 | 1 |
Solution For the spot speed study, first draw a frequency distribution table show below.
| Range | V i | fi | %fi | %∑ fi | fiV i | fi(V i - V m)2 |
| 21-25 | 23 | 2 | 2% | 2% | 46 | 1036.9 |
| 26-30 | 28 | 6 | 5% | 6% | 168 | 1894.5 |
| 31-35 | 33 | 18 | 14% | 20% | 594 | 2935.0 |
| 36-40 | 38 | 25 | 19% | 39% | 950 | 1509.0 |
| 41-45 | 43 | 19 | 15% | 54% | 817 | 145.7 |
| 46-50 | 48 | 16 | 12% | 66% | 768 | 79.6 |
| 51-55 | 53 | 17 | 13% | 79% | 901 | 888.8 |
| 56-60 | 58 | 12 | 9% | 88% | 696 | 1795.1 |
| 61-65 | 63 | 7 | 5% | 94% | 441 | 2078.3 |
| 66-70 | 68 | 4 | 3% | 97% | 272 | 1976.8 |
| 71-75 | 73 | 3 | 2% | 99% | 219 | 2224.5 |
| 76-80 | 78 | 1 | 1% | 100% | 78 | 1038.8 |
| Total | 130 | 100% | 5950 | 17603.0 | ||
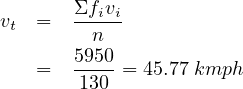
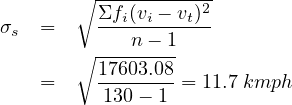
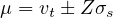 |
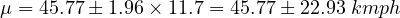 |
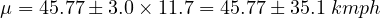 |
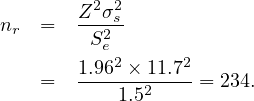
| Parameter | Value |
| Median speed | 43 kmph |
| Modal speed | 38 kmph |
| Pace | 33-43 kmph |
| Vehicles in pace | 34% |
| Mean speed | 45.77 kmph |
| Standard Deviation | 11.7 kmph |
| 85th percentile speed | 58 kmph |
| 15th percentile speed | 32 kmph |
| 98th percentile Speed | 72 kmph |
| Confidence interval | |
| For 95%. | 45.77±22.93 kmph |
| For 99.7% | 45.7725.1 kmph |
| Required sample Size | 234 |
The speed studies are accompanied for eminently logical purposes that will influence what traffic engineering measures are implemented in any given case. The location at which speed measurements are taken must conform to the intentional purpose of the study. The guiding philosophy behind spot speed studies is that measurements should include drivers freely selecting their speeds, unaffected by traffic congestion. For example if driver approaches to a toll plaza, then he has to slow his speed, so this is not suitable location to conduct the study, measurements should be taken at a point before drivers start to decelerate. Similarly, if excessive speed around a curve is thought to be contributing to off-the-road accidents, speed measurements should be taken in advance of the curve, before deceleration begins. It may also be appropriate, however, to measure speeds at the point where accidents are occurring for evaluation with approach speeds. This would allow the traffic engineer to assess whether the problem is excessive approach speed or that drivers are not decelerating sufficiently through the subject geometric element, or a combination of both. A study of intersection approach speeds must also be taken at a point before drivers begin to decelerate. This may be a moving point, given that queues get shorter and longer at different periods of the day.
This chapter has presented the basic concepts of speed studies. Spot speed studies are conducted to estimate the distribution of speeds of vehicle in the traffic stream at a particular position on highway. This is done by recording the speeds of vehicle at the specified location. These data are used to obtain speed characteristics such as mean speed, modal speed, pace, standard deviation and different percentile of speeds. The important factors which should consider during plan of studies is the location of study, time and duration of study. The data sample collected should contain samples size. These gives precision and accuracy of result.
| Speed | Frequency |
| 1- 5 | 9 |
| 6-10 | 16 |
| 11-15 | 32 |
| 16-20 | 48 |
| 21-25 | 23 |
| 26-30 | 9 |
| Obs. No | Speed (kmph) |
| 1 | 55.1 |
| 2 | 40.8 |
| 3 | 32.2 |
| 4 | 47.8 |
| 5 | 64.5 |
| 6 | 53.2 |
| 7 | 58.2 |
| 8 | 66.6 |
| 9 | 36.4 |
| 10 | 53.2 |
| Speed Range (kmph) | Observed | |
| Lower | Upper | Proportion |
| Bound | Bound | |
| 10 | 20 | 0.012 |
| 20 | 30 | 0.178 |
| 30 | 40 | 0.316 |
| 40 | 50 | 0.218 |
| 50 | 60 | 0.108 |
| 60 | 70 | 0.055 |
| 70 | 80 | 0.033 |
| 80 | 90 | 0.022 |
| 90 | 100 | 0.013 |
| 100 | 110 | 0.045 |
Number of observations | 2600 | |
Mean speed in kmph | 40 | |
Standard deviation | 22 | |
Minimum possible speed | 10 | |
I wish to thank several of my students and staff of NPTEL for their contribution in this lecture. I also appreciate your constructive feedback which may be sent to tvm@civil.iitb.ac.in
Prof. Tom V. Mathew
Department of Civil Engineering
Indian Institute of Technology Bombay, India
_________________________________________________________________________
Monday 21 August 2023 12:19:46 AM IST