Transportation networks
Lecture Notes in Transportation Systems Engineering
*IIT Bombay (tvm@civil.iitb.ac.in) January 3, 2019
Contents
_________________________________________________________________________________________
1 Introduction
- Objective: a clear statement of the basic principles of underlying the theory and
application of network flows in transportation.
- Applicable to road traffic, rail, shipping, and airline network.
- Assist in transportation planning and traffic control applications.
- Examples of network representation:
- Road Network
- Traffic Desire Network
2 Graphs: Definitions and Notations
2.1 Directed Graph
- Directed graph [N,L] is a set of N unordered elements and a set of L ordered pairs
of elements of N.
- Number of elements in N and L are n and l respectively.
- N (ni,i = 1, 2,…,n) is the set of node and L (lk(ni,nj), ni ∈ N, nj ∈ N,k = 1, 2,…,l)
is the set of links.
- Here, we assume there is no parallel link.
- If ni = nj then the link is a loop (nodes defining link may or may not be distinct).
- It is common practice to call the nodes ni and nj defining the link lk(ni,nj) as A node
and B node respectively.
- Partial Graph of the directed graph [N,L] is defined as [N,L′] where L′⊆ L. This is
obtained by deleting links.
- Sub Graph of the directed graph [N,L] is defined as [N′,L′] where N′ ⊆ N and
L′ = {(ni,nj)|(ni,nj) ∈ L,ni ∈ N′,nj ∈ N′}. Obtained by deleting nodes and attached
links.
- Complete Graph is graph with at least one link joining any two distinct nodes of N,
that is, ni ∈ N, nj ∈ N, ni≠nj, (ni,nj)
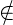 L ⇒ (nj,ni) ∈ L.
L ⇒ (nj,ni) ∈ L.
- Bipartite Graph is a graph in which the set of N nodes is divided into two
complementary set X,X, such that, X ∪X = N and X ∩X = ∅ and L = {(ni,nj)|ni ∈
X, nj ∈X}
2.2 Chain and Cycle
If n1,n2…nr are distinct nodes, then the sequence n1(n1,n2)n2(n2,n3)n3…nr-1(nr-1,nr)nr defines a
chain from origin node n14 to destination node nr. If n1 = nr then chain becomes a cycle. In
figure 1 1 (1,2) 2 (2,3) 3 (3,4) 4 is a chain from node 1 to 4 while 2 (2,3) 3 (3,2) 2 is a cycle from 2
to 2.
2.3 Path and Mesh
If directions of links are not considered chain and cycle becomes path and mesh respectively. If
n1,n2…nr are distinct nodes (ni′,ni+1′) are links, then a path from origin node n1 to destination node
nr is defined by the sequence n1(n1′,n2′)n2…ni(ni′,ni+1′)ni+1…nr) where either ni′ = ni and
ni+1′ = ni+1 (forward link) or ni′ = ni+1 and ni+1′ = ni (reverse link). The path becomes a mesh if
n1 = nr.
2.4 Accessible and connected nodes
In a graph, n1 to nr is accessible if there exists a chain from n1 to nr and is connected if there exists
a path from n1 to nr. If n1 to nr is accessible, that does not imply nr to n1 is accessible, however, if
n1 to nr is connected, that does imply nr to n1 is connected.
A connected directed graph is a graph in which all nodes are connected.
2.5 Cut-Set
If the set of nodes N is partitioned into complementary sets X and X then the sub set L
defined by (X,X) = {(i,j)|(i,j) ∈ L,i ∈ X,j ∈X is called a cut set. Refer to the graph in
figure 1: if X = {1, 2} and X = {3, 4}, then cut set (X,X)={(1,3), (1,4), (2,3), (2,4)} and the
cut set (X,X)={(3,2)}. Cut set has several applications in transportation networks, for
example the road links crossing a screen lines and cordon lines can be modelled as cut
sets.
2.6 Undirected and mixed graphs
The undirected graph [N,L], the elements of L are unordered pair of elements of N and are
denoted as (ni,nj) or (nj,ni). Arrow heads are not required for their representation. Pedestrian link
or two way streets are some examples.
2.7 Tree and Arborescence
A tree denoted by [N,T] is a connected graph with no meshes (directions are ignored). A graph is a
tree if and only if every pair of distinct nodes is connected precisely one path. A spanning
tree of a graph [N,L] is a tree [N,T] which is a partial graph of [N,L], that is, T ⊆ L
When directions are considered, then the tree which consists of chains from home node
to all other nodes is called and Arborescence. Hence, an Arborescence is a directed
graph in which, for a node nr called as the root and any other node ni, there is exactly
one directed path from nr to ni. Spanning tree has application in finding the shortest
path.
3 Flows and Conservation Laws
- When the links of a graph is used to denote flow of vehicles, goods, or pedestrain, then
the graph is referred as a network or transportation network
- Flow then denotes quantity per unity time, the rate at which flow takes place (vehicles
per hour, pedestian per hour, etc.)
- Fundamental to any network dealing with flows (like electrical, or water or
transportation network) is the fact that flows are not lost in the network.
- Kirchhoff’s law state the same concept, but note that we are concerned with the steady
state macroscopic conditions and not valid under microscopic and stocastic conditions.
3.1 Link Flows and Kirchhoff’s Law
Three kind of nodes exist in transporation network:
- Intermediate node: sum of all flows entering the node equals the sum of all flows
leaving the node
- Production Centroid or source: the sum of all flows leaving the node equals the flow
produced at that node
- Attraction Centroid: or sink: the sum of all flows entering the node equals the flows
attracted to that node
Following notations may be stated first:
- fij is the link flow on the directed link (i,j)
- ai is the flow produced at the centroid (i)
- bi is the flow attracted to the centroid (i)
- All flows are assumed to be non-negative (fij, ai, bi ≥ 0)
- A(i) is the set of nodes after node i, defined as:
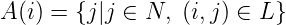 | (1) |
- B(i) is the set of nodes before node i, defined as:
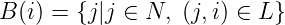 | (2) |
Now, the Kirchhoff’s flow conservation law for a directed transportion network [N; L] can be written as:
The last equation ensures some solution to the problem. Since, the no of links are normally more
than the number of node in typical transportation networks, the number of unknown exceeds the
number of equations and hence there will be mutiple solutions to this problem.
3.1.1 Numerical Illustration
Verify Kirchhoff’s law for the network given in figure 10 for node 2 and 3.
Solution
Node 2: For the node i=2, A(i = 2) = 3, 4 and B(i = 2) = 1, 3
Node 3: The above steps may be repeated.
3.2 Single O-D networks: Link flows
If i = 1 is the origin node and i = n is the destination node, the node 1 is desgnated as the
production zone with g where g is the flow produced and zero flow attracted. Similarly, the node n is
designated as the attraction zone with g where g is the flow attracted and zero flow is
produced.
The conservation equation for such a network can be written as:
where, g denote the flow value, and fij is the flow on link i,j.
Theorem
The net flow across any cut-set (X,X) separating the origin and destination is equal to the flow
value.
3.2.1 Numerical Illustration
Verify the above theorem that the net flow across the cut-set (X,X) separating the origin
1 and destination 4 is equal to the flow value of 7 for the network given in figure 11.
Solution
- The cut set is defined by X = {1, 3} and X = {2, 4}
- The cut-set (X,X) = {(1, 2), (3, 2), (2, 3)}
- The cut-set (X,X) = {(2, 4)}
- The net flow f(X,X) - f(X,X) = 3 + 3 + 2 - 1 = 7.
The conservation equation can be conveniently represented in a matrix form. The node-link
incidence matrix in an n × l matrix E where the rows corresponds to nodes (i)and the column
corresponds to links (j,k) and each cell denoted by δjki defined as:
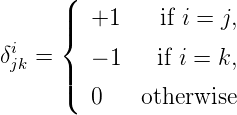 | (7) |
For example ...
and the resultant flow value vector g is
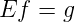 | (8) |
The flow conservation equations () can now be written as:
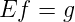 | (9) |
where f is the vector of link flows, g is the O-D vector.
and the resultant flow value vector g is
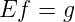 | (10) |
where f is the vector of link flows, g is the O-D vector.
3.3 Multiple O-D Network: Chain Flows
Link flow is superimposition of chain flow. Define:
- fi is the set of links (i = 1, 2…l)
- hj is the set of chains (j = 1, 2…m)
- hj is the chain flow.
The flow value g is then the sum of all chain flows, that is:
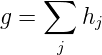 | (11) |
To get the link flow, a term aij is defined as:
 | (12) |
And now the link flow fi is given as:
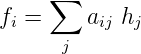 | (13) |
Note that the link flow from chain flow is unique whereas the chain flow from the link flow
is not unique. The above things can be written in a matrix form by first defining a link
chain incident matrix Al×m with aij as it elements. T Then, the link flow vector f is given
as:
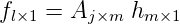 | (14) |
Now, the scalar flow value g can be given as:
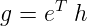 | (15) |
where e is a column vecotor of size m and all elements equals to 1.
3.3.1 Numerical Illustration
For the network given in Figure 12, the chain flows are given below. Find the link flows and the flow
values.
| no | Chains | Chain Flow |
| m1 | (1,2) (2,3) (3,4) | 1 |
| m2 | (1,2) (2,4) | 2 |
| m3 | (1,3) (3,2) (2,4) | 3 |
| m4 | (1,3) (3,4) | 1 |
| |
Solution
The link chain incident matrix Al×m can be written as:
Hence, the flow vector f is given as: And for getting the flow value, the vector e is defined as: and g is given as:
3.4 Costs and Capacities
The cost could be time, distance, delay, or disutility etc. The following notations and definitions are
normally used in transporation network analysis.
- Link cost: cij(fij) is the average cost or cost per unit flow. The unit link cost is function
of the flow on that link.
- Total link cost: which is flow dependent can be defined as fij × cij(fij).
- Route cost: on a chain or a path from origin to destination is the sum of all the link costs of
the links that define the route can be expressed as:
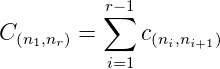 | (16) |
- Route cost with turn penalties: is defined as:
![r∑-1
C = [c + p ]
(n1,nr) (ni,ni+1) ((ni,ni+1),(ni+1,ni+2))
i=1](web24x.png) | (17) |
where p((ni,ni+1),(ni+1,ni+2)) is the penalty for turning from the link (ni,ni+1) to (ni+1,ni+2).
- Network cost:
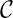 is the sum of all the total link cost of all the links of the network, and is given
as:
is the sum of all the total link cost of all the links of the network, and is given
as:
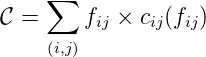 | (18) |
- If a link is prohibited for movement, it can represented by putting cij = ∞ and if a turn is
prohibited, it can be represented by p(.) = ∞
4 Network Algorithms
4.1 Minimal spanning tree
In a connected weighted graph, all spanning trees have n-1 edges and will have minimum or
maximum sum of the weights. Tow algorithms are proposed: Prims algorithm and Kruskal’s
algorithm. ‘
4.1.1 Prims algorithm
Prims algorithm grows a spanning tree from a given vertex of a connected weighted graph G,
iteratively adding the cheapest edge from a vertex already reached to a vertex not yet
reached, finishing when all the vertices of G have been reached. Break tie arbitrarily.
4.1.2 Numerical Example
Find the minimum spanning tree of the network given in figure 14
Solution
- Start with node 1, N={1}, T={Φ}
- Node 1 can be connected by nodes 2, 3, and 4, having weights 12, 17, and 10
- Minimum weight is 10, for node 4. So N={1,4}, T={(1,4)}
- Node 1 can be connected by nodes 2 and 3, having weights 12 and 17
- Node 4 can be connected by nodes 3 and 5, having weights 14 and 19
- Minimum weight is 12, for node 2. So N={1,4,2}, T={(1,4),(1,2)}
- Node 1 can be connected by node 3, having weight 17
- Node 4 can be connected by nodes 3 and 5, having weights 14 and 19
- Node 2 can be connected by nodes 3 and 5, having weights 18 and 16
- Minimum weight is 14, for node 3. So N={1,4,2,3}, T={(1,4),(1,2),(3,4)}
- Node 1 can be connected by no nodes without loop
- Node 4 can be connected by node 5, having weight 19
- Node 2 can be connected by node 5, having weight 16
- Node 3 can be connected by node 5, having weight 11
- Minimum weight is 11, for node 3. So N={1,4,2,3}, T={(1,4),(1,2),(3,4),(3,5)} W=49.
4.1.3 Kruskal’s algorithm
The main concept of this algorithm is to maintain an acyclic spanning sub-graph H, enlarging it by
edges with low weight to form a spanning tree. Consider edges in non-descending order of weight,
breaking ties arbitrarily.
Example
Find the minimum spanning tree of the network given in figure 14
Solution
- Sort the links in the descending order of weights results in
- 19 (4,5); 18 (2,3); 17 (1,3); 16 (2,5); 14 (3,4); 12 (1,2); 11 (3,5); and 10 (1,4)
- T=(1,4) W=10
- T=(1,4),(3,5) W=10+11
- T=(1,4),(3,5),(1,2), W=10+11+12
- T=(1,4),(3,5),(1,2),(3,4), W=10+11+12+14=47
4.2 Dijkstra’s shortest path algorithms
This algorithm finds the shortest path for a graph from a starting node to every other node. The
algorithm is given in Figure 17 and each step is described below.
- Input to the algorithm is a graph G(N,L) with nonnegative edge weights and a starting
vertex u. The destination vertex v The weight of the edge xy is w(xy) and w(xy) = ∞
if xy is not an edge.
- Initilize step involves defining the solution set S with the starting vertex as the only
element. Further, a variable t associated with vertex u is defined and set its value to
zero.
- Iteration starts by selecting all possible edges defined by the starting node v from the
set S and the end node z not in the set S. For each of the end node z, the total cost
up to that node is computed by adding the total cost upto node v computed in previos
iteration and the weight of the edge (xy), that is t(z) = t(v) + w(xy). Find the node
which has minimum cost and add that node to the solution set S.
- Termination of the algorithm happens when all the node becomes element of the
solution set S or the destination node is reached.
4.2.1 Numerical Example
Find the minimum shortest path of the graph given in figure 18 from the node u.
Solution
Table 1: Solution to the shortest path algorithm
|
|
|
|
|
|
|
| {S} | v | vz | t(z) | t*(z) | z* | {S*} |
|
|
|
|
|
|
|
| u | u | ua | 0+1=1 | 1 | a | ua |
| | | ub | 0+3=3 | | | |
|
|
|
|
|
|
|
| ua | u | ub | 0+3=3 | 3 | b | uab |
| | a | ad | 1+5=6 | | | |
| | | ac | 1+4=4 | | | |
|
|
|
|
|
|
|
| uab | a | ad | 1+5=6 | | | |
| | | ac | 1+4=5 | 5 | c | uabc |
| | b | bd | 3+4=7 | | | |
| | | bc | 3+5=8 | | | |
|
|
|
|
|
|
|
| uabc | a | ad | 1+5=6 | 6 | d | uabcd |
| | b | bd | 3+4=7 | | | |
| | c | ce | 5+6=11 | | | |
|
|
|
|
|
|
|
| uabcd | d | de | 6+2=8 | 8 | e | uabcde |
| | c | de | 5+6=11 | | | |
|
|
|
|
|
|
|
| |
Note:
t(z) = t(v) + w(vz),
t*(z) = min t(z)
4.2.2 Numerical Example 2
Find the minimum shortest path of the graph given in figure 20 from the node O to the destination
node T.
Solution
The solution is given in Figure 21.
5 Network Optimization
5.1 Maximum Flow Problem
5.2 Minimum Cost Flow Problem
5.3 Transportation Problem
5.4 Assignment Problem
5.5 Traveling Salesman Problem
6 Travelling salesman problem (TSP)
6.1 Introduction
Travelling salesman problem (TSP) consists of finding the shortest rout e in complete weighted
graph G with n nodes and n(n-1) edges, so that the start node and the end node are identical and
all other nodes in this tour are visited exactly once.
6.2 Formulation
Let C be the matrix of shortest distances (dimension nxn), where n is the number of nodes of
graph G(NL). The elements of matrix C represents the shortest distances between all pairs of
nodes (i,j),i,j = 1, 2,…,n. The travelling salesman problem can be formulated in the
category programming binary, where variables are equal to 0 or 1, depending on the fact
whether the route from node i to node j is realized (xij = 1) or not (xij = 0). Then, the
mathematical formulation of TSP is as follows (the idea of this formulation is to assign the
numbers 1 through n to the nodes with the extra variables ui, so that this numbering
corresponds to the order of the nodes in the tour. It is obvious that this excludes sub-tours, as a
sub-tour excluding the node 1 cannot have a feasible assignment of the corresponding ui
variables):
 |
(19)
(20)
(21)
(22)
(23)
(24)
|
The constraint 23 ensures there is no sub-trours.
Exercises
- Not Available
References
- Frederick S Hillier and Gerald J Lieberman. Introduction to Operations Research.
Tata McGraw-Hill Publishers, New Delhi, 2001.
- Renfrey B Potts and Robert M Oliver. Flows in transportation networks. Academic
Press, New York, 1972.
- Douglas B West. Introduction to graph theory. Pearson education Asia, New Delhi,
India, 2001.
Acknowledgments
I wish to thank several of my students and staff of NPTEL for their contribution in this lecture. I also
appreciate your constructive feedback which may be sent to tvm@civil.iitb.ac.in
Prof. Tom V. Mathew
Department of Civil Engineering
Indian Institute of Technology Bombay, India
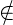 L ⇒ (nj,ni) ∈ L.
L ⇒ (nj,ni) ∈ L.
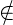 L ⇒ (nj,ni) ∈ L.
L ⇒ (nj,ni) ∈ L.
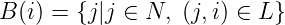

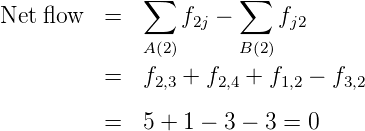
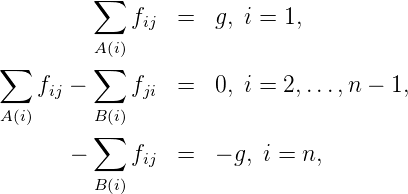
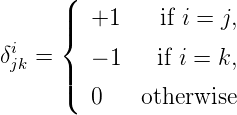

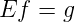
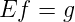
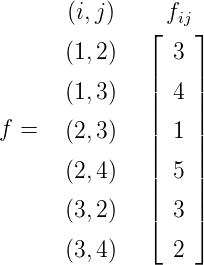
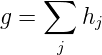

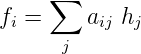
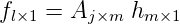
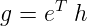
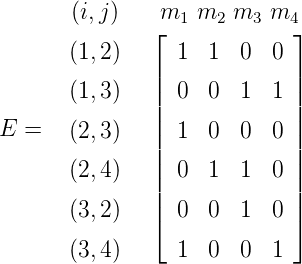
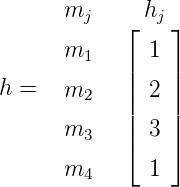
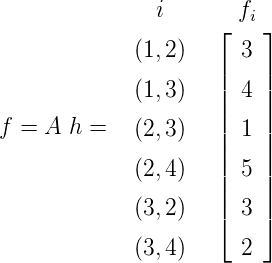
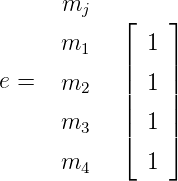
![⌊ ⌋
1
|| ||
g = eTh = [1 1 1 1] × || 2 || = 7.
| 3 |
⌈ ⌉
1](web22x.png)
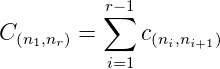
![r∑-1
C = [c + p ]
(n1,nr) (ni,ni+1) ((ni,ni+1),(ni+1,ni+2))
i=1](web24x.png)