As already noted in the previous chapter that vehicle arrivals can be modelled in two inter-related ways; namely modelling how many vehicle arrive in a given interval of time, or modelling what is the time interval between the successive arrival of vehicles. Having discussed in detail the former approach in the previous chapter, the first part of this chapter discuss how a discrete distribution can be used to model the vehicle arrival. Traditionally, Poisson distribution is used to model the random process, the number of vehicles arriving a given time period. The second part will discuss methodologies to generate random vehicle arrivals, be it the generation of random headways or random number of vehicles in a given duration. The third part will elaborate various ways of evaluating the performance of a distribution.
Suppose, if we plot the arrival of vehicles at a section as dot in a time axis, it may look like Figure 1.
Let h1, h2, ... etc indicate the headways, then as mentioned earlier, they take some real values. Hence, these headways or inter arrival time can be modelled using some continuous distribution. Also, let t1, t2, t3 and t4 are four equal time intervals, then the number of vehicles arrived in each of these interval is an integer value. For example, in Fig. 1, 3, 2, 3 and 1 vehicles arrived in time interval t1, t2, t3 and t4 respectively. Any discrete distribution that best fit the observed number of vehicle arrival in a given time interval can be used. Similarly, any continuous distribution that best fit the observed headways (or inter-arrival time) can be used in modelling. However, since these process are inter-related, the distributions that describe these relations should also be inter-related for better explanation of the phenomenon. Interestingly, there exist distributions that meet the above requirements. First, we will see the distribution to model the number of vehicles arrived in a given duration of time. Poisson distribution is commonly used to describe such a random process. The probability density function of the Poisson distribution is given as:
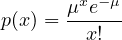 | (1) |
where p(x) is the probability for x events will occur in the time interval, and μ is the expected rate of occurrence of that event in that interval. Some special cases of this distribution is given below.
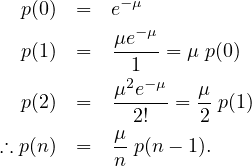
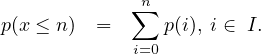
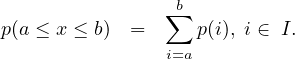
The hourly flow rate in a road section is 120 vph. Use Poisson distribution to model this vehicle arrival.
Solution:
The flow rate is given as (μ) = 120 vph = 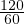 = 2 vehicle per minute. Hence, the
probability of zero vehicles arriving in one minute p(0) can be computed as follows:
= 2 vehicle per minute. Hence, the
probability of zero vehicles arriving in one minute p(0) can be computed as follows:
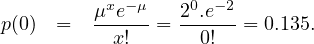
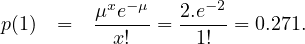
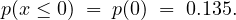
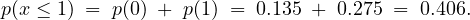
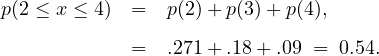
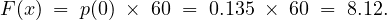
| n | p(n) | p(x ≤ n) | F(n) |
| 0 | 0.135 | 0.135 | 8.120 |
| 1 | 0.271 | 0.406 | 16.240 |
| 2 | 0.271 | 0.677 | 16.240 |
| 3 | 0.180 | 0.857 | 10.827 |
| 4 | 0.090 | 0.947 | 5.413 |
| 5 | 0.036 | 0.983 | 2.165 |
| 6 | 0.012 | 0.995 | 0.722 |
| 7 | 0.003 | 0.999 | 0.206 |
| 8 | 0.001 | 1.000 | 0.052 |
| 9 | 0.000 | 1.000 | 0.011 |
| 10 | 0.000 | 1.000 | 0.011 |
The shape of this distribution can be seen from Figure 2 and the corresponding cumulative distribution is shown in Figure 3.
For simulation purposes, it may be required to generate number of vehicles arrived in a given interval so that it follows typical vehicle arrival. This is the reverse of computing the probabilities as seen above. The following steps give the procedure:
The steps 3 to 5 can be repeated for required number of intervals.
Generate vehicles for ten minutes if the flow rate is 120 vph.
Solution The first two steps of this problem is same as the example problem solved earlier and the resulted from the table is used. For the first interval, the random number (X) generated is 0.201 which is greater than p(0) but less than p(1). Hence, the number of vehicles generated in this interval is one (ni = 1). Similarly, for the subsequent intervals. It can also be computed that at the end of 10th interval (one minute), total 23 vehicle are generated. Note: This amounts to 2.3 vehicles per minute which is higher than given flow rate. However, this discrepancy is because of the small number of intervals conducted. If this is continued for one hour, then this average will be about 1.78 and if continued for then this average will be close to 2.02.
| No | X | n |
| 1 | 0.201 | 1 |
| 2 | 0.714 | 3 |
| 3 | 0.565 | 2 |
| 4 | 0.257 | 1 |
| 5 | 0.228 | 1 |
| 6 | 0.926 | 4 |
| 7 | 0.634 | 2 |
| 8 | 0.959 | 5 |
| 9 | 0.188 | 1 |
| 10 | 0.832 | 3 |
| Total | 23 | |
One can generate random variate following negative exponential distribution rather simply due to availability of closed form solutions. The method for generating exponential variates is based on inverse transform sampling:
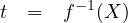
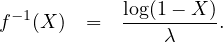
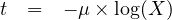
Simulate the headways for 10 vehicles if the flow rate is 120 vph.
Solution Since the given flow rate is 120 vph, then the mean headway (μ) is 30 seconds. Generate a random number between 0 and 1 and let this be 0.62. Hence, by the above equation, t = 30 × (-log(0.62)) = 14.57. Similarly, headways can be generated. The table below given the generation of 15 vehicles and it takes little over 10 minutes. In other words, the table below gives the vehicles generated for 10 minutes. Note: The mean headway obtained from this 15 headways is about 43 seconds; much higher than the given value of 30 seconds. Of, course this is due to the lower sample size. For example, if the generation is continued to 100 vehicles, then the mean would be about 35 seconds, and if continued till 1000 vehicles, then the mean would be about 30.8 seconds.
| No | X | t | ∑ t |
| 1 | 0.62 | 14.57 | 14.57 |
| 2 | 0.17 | 53.70 | 68.27 |
| 3 | 0.27 | 39.14 | 107.41 |
| 4 | 0.01 | 157.36 | 264.77 |
| 5 | 0.26 | 40.01 | 304.78 |
| 6 | 0.47 | 22.72 | 327.5 |
| 7 | 0.96 | 1.38 | 328.88 |
| 8 | 0.24 | 42.76 | 371.64 |
| 9 | 0.59 | 15.94 | 387.58 |
| 10 | 0.45 | 24.05 | 411.63 |
| 11 | 0.26 | 40.82 | 452.45 |
| 12 | 0.11 | 67.39 | 519.84 |
| 13 | 0.10 | 69.33 | 589.17 |
| 14 | 0.73 | 9.63 | 598.8 |
| 15 | 0.31 | 34.74 | 633.54 |
The mathematical distribution such as negative exponential distribution, normal distribution, etc needs to be evaluated to see how best these distributions fits the observed data. It can be evaluated by comparing some aggregate statistics as discussed below.
One of the easiest ways to compute the mean and standard deviation of the observed data and compare with mean and standard deviation obtained from the computed frequencies. If pic is the computed probability of the headway is the ith interval, and N is the total number of observations, then the computed frequency of the ith interval is given as:
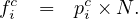
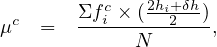
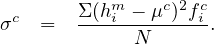
The Chi-square value (X2) can be computed using the following formula:
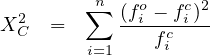
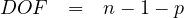
Compute the X2 statistic of the following distribution, where N = 2434.
| h | h + dh | pio | pic |
| 0.0 | 1 | 0.012 | 0.249 |
| 1.0 | 2 | 0.178 | 0.187 |
| 2.0 | 3 | 0.316 | 0.140 |
| 3.0 | 4 | 0.218 | 0.105 |
| 4.0 | 5 | 0.108 | 0.079 |
| 5.0 | 6 | 0.055 | 0.060 |
| 6.0 | 7 | 0.033 | 0.045 |
| 7.0 | 8 | 0.022 | 0.034 |
| 8.0 | 9 | 0.013 | 0.025 |
| 9.0 | > | 0.045 | 0.076 |
| Total | 1 | 1 | |
Solution:
The given headway range and the observed probability is given in column (2),
(3) and (4). The observed frequency for the first interval (0 to 1) can be computed
as the product of observed probability pi and the number of observation (N) i.e.
fio = pio ×N = 0.012 × 2434 = 29.21 as shown in column (5). Now the computed frequency
for the first interval (0 to 1) is the product of computed probability and the number of
observation (N) i.e. fic = pic × N = 0.249 × 2434 = 441.21 as shown in column (7). The
χ2 value can be computed as 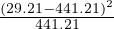 = 384.73. Similarly, all the rows are
computed and the total χ2 value is obtained as 1825.52. A chi-square table gives X2
values for various degree of freedom. The degree of freedom (DOF) is given as:
DOF = n - 1 - p = 10 - 1 - 1 = 8, where n is the number of intervals (10), and p is the
number of parameter (1 because it is exponential distribution). Now at a significance level of
0.05 and DOF 8, from the table, XT2 = 15.5. Since χT2 < χC2 hence reject that the observed
frequency follows exponential distribution.
= 384.73. Similarly, all the rows are
computed and the total χ2 value is obtained as 1825.52. A chi-square table gives X2
values for various degree of freedom. The degree of freedom (DOF) is given as:
DOF = n - 1 - p = 10 - 1 - 1 = 8, where n is the number of intervals (10), and p is the
number of parameter (1 because it is exponential distribution). Now at a significance level of
0.05 and DOF 8, from the table, XT2 = 15.5. Since χT2 < χC2 hence reject that the observed
frequency follows exponential distribution.
| No | h | h + dh | pio | fio | pic | fic | χ2 |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) |
| 1 | 0.0 | 1 | 0.012 | 29.21 | 0.249 | 441.21 | 384.73 |
| 2 | 1.0 | 2 | 0.178 | 433.25 | 0.187 | 361.23 | 14.36 |
| 3 | 2.0 | 3 | 0.316 | 769.14 | 0.140 | 295.75 | 757.73 |
| 4 | 3.0 | 4 | 0.218 | 530.61 | 0.105 | 242.14 | 343.67 |
| 5 | 4.0 | 5 | 0.108 | 262.87 | 0.079 | 198.25 | 21.07 |
| 6 | 5.0 | 6 | 0.055 | 133.87 | 0.060 | 162.31 | 4.98 |
| 7 | 6.0 | 7 | 0.033 | 80.32 | 0.045 | 132.89 | 20.79 |
| 8 | 7.0 | 8 | 0.022 | 53.55 | 0.034 | 108.80 | 28.06 |
| 9 | 8.0 | 9 | 0.013 | 31.64 | 0.025 | 89.08 | 37.03 |
| 10 | 9.0 | > | 0.045 | 109.53 | 0.076 | 402.34 | 213.10 |
| Total | 1 | 1 | 1825.52 | ||||
The chapter covers three aspects: modeling vehicle arrival using Poisson distribution, generation of random variates following certain distribution, and evaluation of distributions. Specific evaluation include comparing the mean and standard deviation at macro level and using chi-square test which is essentially a micro-level comparison.
| Vehicle arriving | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| in 20s interval | |||||||
| Frequency | 17 | 31 | 12 | 24 | 10 | 6 | 0 |
Give the flow rate in vehicle per hour and a total duration of simulation in seconds, this program computes the random headway following negative exponential distribution
Modify the flow rate and duration in the program itself. To compile in linux use gcc prog.c -lm -o prog.exe and to run .\prog.exe.
I wish to thank several of my students and staff of NPTEL for their contribution in this lecture. I also appreciate your constructive feedback which may be sent to tvm@civil.iitb.ac.in
Prof. Tom V. Mathew
Department of Civil Engineering
Indian Institute of Technology Bombay, India
_________________________________________________________________________
Thursday 31 August 2023 12:12:58 AM IST