Figure 1: Open Toll System
Toll tax is collected to recover the total capital outlay which includes the cost of construction, repairs, maintenance, expenses on toll operation and interest on the outlay. The new facility thus constructed should provide reduced travel time and increased level of service. In India most of the highway projects are given on PPP basis, i.e. Public Private Partnership. In this the private organization finances and constructs the facility and recovers the capital from the users in the form of toll tax. This tax is collected for a reasonable period of time after which the facility is surrendered to the public. Of late, toll tax is being levied on parking of vehicles in the urban centers in a move to decongest the streets and reduce the pollution levels. This concept is known as Congestion Pricing.
There are two types of toll collection systems available. These are: (i) Open Toll System, and (ii) Closed Toll System.
In an open toll system, not all patrons are charged a toll. In such a system, the toll plaza is generally located at the edge of the urban area, where a majority of long distance travelers are committed to the facility, with a minimum likelihood of switching to the parallel free route, or at the busiest section of the toll way [2]. Patrons are identified by their category and pay a fixed toll for it. The local traffic around the plaza either gets rebate or can use a service lane. The general layout of an open toll collecting system is highlighted in Fig. 1.
In a closed toll system, patrons pay the toll based on miles of travel on the facility and category of vehicle. There are no free-rides. In a closed toll system, plazas are located at all the entry and exit points, with the patron receiving a ticket upon entering the system. Upon exiting, patron surrenders the ticket to the collector and is charged a prescribed fee based on category of vehicle and distance travelled [2]. It has just two stops for the vehicles whereas open system can have multiple stops. But closed system is expensive to construct than open system. The general layout of an open toll collecting system is highlighted in Fig. 2.
There are three methods of toll collection available. These are: (i) Manual, (ii) Automatic, and (ii) Electronic.
Manual toll collection is most widely used collection method in India. It requires a toll collector or attendant. Based on the vehicle classification, cash toll is received by the collector. The collector, who also dispenses change, may accept and sell scrip, tickets, coupons, making an entry of the vehicle in the system and issuing receipt to the patron [2]. Due to manual intervention, the processing time is highest.
Automatic toll collection is based on the use of Automated Coin Machine (ACM). These accept both coins and tokens issued by the operating agency. Depending on the toll rate, the use of automated coin or token collection instead of manual collection reduces transaction and processing time as well as the operating cost.
Electronic Toll Collection (ETC) is a system that automatically identifies a vehicle equipped with a valid encoded data tag or transponder as it moves through a toll lane or checkpoint. The ETC system then posts a debit or charge to a patron’s account, without the patron having to stop to pay the toll. ETC increases the lane throughput because vehicles need not stop to pay the toll.
Some of the basic terms that will be used in the chapters to come have been discussed in this section. Following are the terms and their definitions:
The entire toll plaza area can be divided into two areas namely queueing and the merging area. The vehicles line up to pay the toll in the queueing area. The vehicles wait for their turn to pay the toll at the toll booth. The delay is called as the queueing delay. Similarly, once the vehicle crosses the toll booth, the number of lanes reduces from number of tollbooths to the original width of the highway. A vehicle travelling in a lane has to wait or slow down to allow another vehicle in the adjacent lane to pass. These kind of delays are termed as merging delays. We will apply Queueing Theory to ascertain the delays in both the areas. Keeping the total delay time to be minimum, we find the optimal number of tollbooths for the system. The time wasted at the tollbooth (WA) is given by the equation. 1:
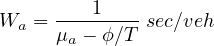 | (1) |
where, μa = Service rate at a tollbooth (veh/hr), ϕ = Total traffic flow (veh/hr), T = Number of
tollbooths
Similarly, the time wasted at merging area is calculated using the following logic. If there are T
tollbooths which are finally merged into N lanes of highway then the number of merging
points are given by (T - N) (see Fig. 4).
From Fig. 4 we can see that in a toll plaza with a side merging layout which has T tollbooths, the first merging point takes a stream coming from 2 tollbooths, and the second merging point would take a stream from 3. By Little’s theorem, the average waiting time in the system tsys(λ) is given by the equation. 2:
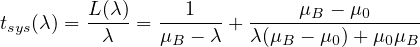 | (2) |
The average wasted time of a driver at a merging point is the difference between tsys and the time he or she would spend on a normal lane. The expected time a driver spends when no merging happens is 1∕μ0. Hence, the average wasted time is given by the equation. 3.
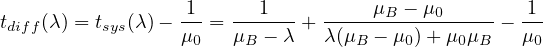 | (3) |
where, μB = Service rate when merging of vehicles takes place (veh/hr), μ0 = Service rate
when no merging of vehicles takes place (veh/hr), λ = Vehicle arrival rate = (k∕T) ×ϕ (veh/hr),
k = No. of conflicting lanes at a merging point. k has a range between [2,T - N + 1]
The above formula gives the average wasted time of a driver at each merging point. The
overall wasted time is the weighted sum of all the wasted time at each merging point, where
the corresponding weight is the probability for a driver to reach that point. The overall wasted
time (WB) can be calculated using the equation. 4.
 | (4) |
As per the optimal toll plaza configuration, we need to keep the total delay time as minimum [4]. The Total Wasted Time (Wtotal) for the vehicle (Tollbooth + Merging) is given by the equation. 5:
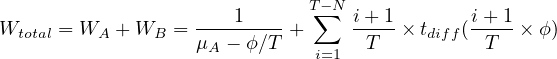 | (5) |
Calculate the Total delay time in toll plaza if the total no of tolls are 3 on a single-lane highway. The total traffic flow on the highway is 800 veh/hr. Assume the following data: Service rate of Tollbooth = 400 veh/hr; Service rate when merging of vehicles takes place =1500 veh/hr; Service rate when no merging of vehicles takes place =2500 veh/hr
Solution:
The following data has been given to us in the problem: N=1 lane; Ø= 800 veh/hr; μA =
400 veh/hr; μB = 1500 veh/hr; μ0 = 2500 veh/hr. Our aim is to determine the total delay time
in toll plaza. From eqn above ; WA =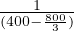 
=0.0075 hr/veh = 27 sec/veh. It means that
the wasted time at the tollbooth is 27 sec/veh. Now we move on to find the overall wasted time
in the merging area (WB). To find that, first we need to find the wasted time at each merging
point which can be calculated using the equation. Now, eqn uses a term k in it which
signifies the number of conflicting lanes at each merging point. k ranges between [2,
T-N+1]. Therefore in this case (T=3) k lies between [2, 4-1+1], i.e. [2,3] When K=2:
Hence, λ at first merging point = (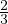
) × 800 = 533.3veh∕hr. From eqn above, for
(λ = 533.33)
Tdiff =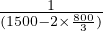 
+ ![(1500- 2500)
[2×-8030(1500--2500)+1500×2500]](web8x.png)
-
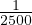= 1.166 sec.
WB for the 1st merging point = (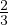
) × 1.166 = 0.777sec When K=3: (
)
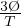Tdiff =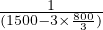 
+ 
×
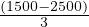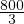(1500 - 2500) + 1500 × 1500 -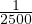
tsys = 2.48 sec. WB for the 2st merging point =(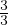
) × 2.48 = 2.48sec. Total WB=0.777+2.48.
WB= 3.257 sec. Wtotal=WA+WB=27.0+3.257. Total delay time Wtotal = 30.257
sec.
Calculate the optimum number of tollbooths to be installed on a toll plaza, proposed to be built on a single-lane highway. The total traffic flow on the highway is 900 veh/hr. Assume the following data: Service rate of Tollbooth = 350 veh/hr; Service rate when merging of vehicles takes place = 1184.9 veh/hr; and Service rate when no merging of vehicles takes place = 3017.1 veh/hr.
Solution: The following data has been given to us in the problem: N=1 lane; ϕ = 900 veh/hr; μA = 350 veh/hr; μB = 1184.9 veh/hr; μ0 = 3017.1 veh/hr Our aim should be to determine the total vehicle delays for different values of tollbooths (T). The value of T corresponding to which the delay time in minimum is the optimal condition. Let us initially start with T=4; From equation. 1; WA = 1/(350 – 900/4) = 0.008 hr/veh = 28.8 sec/veh. It means that the wasted time at the tollbooth is 28.8 sec/veh. Now we move on to find the overall wasted time in the merging area (WB). To find that, first we need to find the wasted time at each merging point which can be calculated using the equation. 3. Now, equation. 3 uses a term k in it which signifies the number of conflicting lanes at each merging point. It can be seen from figure 4 that k ranges between [2,T - N + 1]. Therefore in this case (T=4) k lies between [2, 4-1+1], i.e. [2,4]. Hence, λ at first merging point = (2/4) * 900 = 450 veh/hr. From equation. 3, (λ = 450)
Tdiff = 1∕(1184.9-2×900∕4)+(1184.9-3017.1)∕[2×900∕4(1184.9-3017.1)+1184.9×3017.1]-1∕3017.1 = 1.307 sec.
Similarly, λ at second merging point = (3/4) * 900 = 675 veh/hr and λ at third merging point = (4/4) * 900 = 900 veh/hr. Using equation. 3, the values of tdiff can be found out at second and third merging points. tdiff at second merging point, tdiff (λ=675) = 3.046 sec. tdiff at third merging point, tdiff (λ=900) = 8.018 sec. Now the overall wasted time in merging (WB) is given by the equation. 4 which is the product of the weighted mean of the merging point with the tdiff values. Hence, WB = (2/4) * 1.307 + (3/4) * 3.046 + (4/4) * 8.018 = 6.176 sec. Now, Wtotal can be calculated from equation. 5 which is sum of WA and WB. Wtotal = 28.8 + 6.176 = 34.976 sec. So, for the case of T=4, the total wasted time is 34.976 secs. Following the same procedure to calculate Wtotal for different values of T. For faster calculation purposes, we can use Microsoft Excel to compute the values of WA, tdiff, WB and Wtotal. Following are the wasted times for different vaules of T. We can clearly see that the total delay is minimum for the configuration T=6. Hence 6 tollbooths is the optimal solution for the given highway facility.
| T | WA | Tsys | WB | Wtotal |
| 4 | 28.8 | 12.371 | 6.176 | 34.976 |
| 6 | 18 | 16.403 | 13.839 | 31.839 |
| 8 | 15.15 | 20.436 | 16.805 | 31.955 |
| 10 | 13.846 | 24.476 | 19.815 | 33.661 |
The Concessionaire shall provide required number of Toll Plazas for collection of toll as per the Concession Agreement. The fee collection system shall be speedy, efficient and user friendly. The design of the Toll Plazas should be such that they are aesthetically pleasing and efficient and the fee collection staff should be quick, courteous and adequately trained before deployment.
Fig. 5 shows the general toll plaza geometry of a 2+2 lane toll plaza. Initially, the numbers of lanes become equal to the number of tollbooths, which is equal to three in Fig. 5, in the queueing area. After the vehicle crosses the tollbooth, the number of lanes merges back to the original width of the highway, i.e. two-lane. A lane for the extra wide and the exempted vehicles is provided at the left hand side of the highway. Some extra space is also maintained for the scope of future plaza expansion. The design specifications for the design of the flared portions are as listed below:
As discussed previously, tollbooths are erected to collect the tax from the road users. The number of tollbooths depends on the flow of vehicles on the facility. Following guidelines are generally followed while deciding the number of toll lanes in a toll plaza:
| Forecast Traffic | ||||
| (in vehicles/day) total | 6% | 7% | 8% | 9% |
| of both directions | ||||
| Less than 7000 | 2 | 2 | 2 | 2 |
| 7000-12000 | 2 | 2 | 3 | 3 |
| More than 12000 | 3 | 3 | 4 | 4 |
As discussed earlier, there are three methods of toll collection. Out of them, the manual method is the most time consuming whereas the delays are minimum for electronic system. Following measures are adopted for making the toll collection process a faster one.
A tollbooth is that location of the toll plaza where the tax is actually paid. This section lays emphasis on the procedures involved in the construction of a tollbooth.
The traffic signs inform the users about the approaching toll plaza, prices for different categories. Some of the guidelines laid down are:
The road markings help in channelizing the movement of vehicles in a toll plaza. These comprise of the diagonals, lanes and chevron markings. Following specifications are followed while doing the road markings.
Toll plaza lighting needs due consideration because user should be able to spot the existence of a toll plaza from a distance at night. The specifications for different types of lighting provided at a toll plaza are listed below:
Toll is a fee collected for the use of the road, bridge, tunnel, etc. to recover the total capital outlay which includes interest on outlay, cost of repairs, maintenance and also expenses on collection of toll. Hence the amount of toll should not exceed the benefits which the user receive while using the toll road. The benefits are due to savings in travel time, travel cost, increase in comfort and convenience. The toll structure should be fixed in such a way that investments and expenses are recovered within a reasonable period of time. The product of optimum toll rate and traffic volume finally determines the gross toll revenue.
Two important factors determine the toll rates. They are:
As mentioned above the toll rates should not be more than savings derived by the road user by using the facility. The savings will be perceived differently by people of different category and people using different modes. For public transport user, he/she is not concerned with vehicle operating cost. Instead, he/she is concerned with the fare to be paid for the unit distance travelled. But for private mode, the user is concerned with the vehicle operating cost and travel time saved. Travel distance, travel time and toll are taken as deterrence measure. Maximum limit of toll as a deterrence is found, beyond which the suggested shortest path becomes uneconomical.
Two factors are to be considered before fixing the optimum toll. They are:
Toll rates of all the vehicles are obtained after including the maintenance cost and the interest on construction cost to the total outlay cost [1].
From the above discussions we can conclude that toll tax is a fee which is used for the use of a newly constructed facility to recoup the total capital outlay. The private organization builds, operates and then transfers the facility after a projected period of time. The Electronic Toll Collection (ETC) system is the most efficient method of toll collection with minimum delays. But due to its high installation cost it’s not that prevalent in India. We can find the optimum number of tollbooths by applying queueing theory to ascertain the delays in both queueing and merging areas. The optimum number of tollbooths should minimize the overall delay time. The toll plaza design should be done in accordance with the Indian Standard Codes available. Toll prices are set in a way that they attract maximum number of users and the agency should be able to recover the cost within specified period of time.
I wish to thank several of my students and staff of NPTEL for their contribution in this lecture. Specially, I wish to thank my student Mr. Neeraj Saxena for his assistance in developing the lecture note, and my staff Ms. Reeba in typesetting the materials. I also appreciate your constructive feedback which may be sent to tvm@civil.iitb.ac.in
Prof. Tom V. Mathew
Department of Civil Engineering
Indian Institute of Technology Bombay, India
_________________________________________________________________________
Thursday 28 September 2023 11:40:30 AM IST
