
System Optimal AssignmentTrip Assignment
Theory
System Optimal AssignmentWardrop (1952) proposed an alternative way of assigning traffic onto a network and this is usually referred to as his second principle: Under social equilibrium condition traffic should be arranged in congested networks in such a way that the average (or total) travel cost is minimised.
This is a design principle, in contrast with his first principle which endeavours to model the behavior of individual driver trying to minimize their own trip costs. The second principle is oriented towards transport planners and engineers trying to manage traffic to minimize travel costs and therefore achieve an optimum social equilibrium. In general the flows resulting from the two principles are not the same but one can only expect, in practice, traffic to arrange itself following an approximation to Wardrop's first principle, i.e. selfish or users' equilibrium.
Obviously, this is not a behaviourally realistic model, but it can be useful to transport planners and engineers, trying to manage the traffic to minimise travel costs and therefore achieve an optimum social equilibrium.
$$\nonumber Minimize\ Z\ =\ \sum\limits_{a} x_a t_a(x_a)$$ $$\nonumber Subject\ to\ \sum\limits_{k} f_k^{rs}\ =\ q_{rs}\ \: \ \forall r,s $$ $$\nonumber x_a = \sum\limits_{r}\sum\limits_{s}\sum\limits_{k} \delta_{a,k}^{rs} f_k^{rs}\ \:\ \forall a $$ $$\nonumber f_k^{rs}\ \geqslant 0\ \:\ \forall k,r,s $$ $$\nonumber x_a\ \geqslant 0\ \:\ a\epsilon A$$
$x_a$ equilibrium flows in link $a$, $t_a$ travel time on link $a,\ f_k^{rs}$ flow on path $k$ connecting O-D pair r-s, $q_{rs}$ trip rate between $r$ and $s$.
User Equilibrium and System Optimization
- UE and SO are similar if congestion is ignored.
- If the link performance function is independent of link flows then UE objective function is similar to SO objective function.
- A network with low flow has small marginal link cost as a result UE and SO flows are similar.
Example
To demonstrate how the most common assignment works, an example network is considered. This network has two nodes having two paths as links.
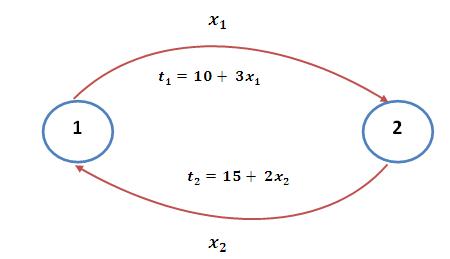
Lets take a case where travel time functions for both the links is given by:
$t_1=10+3x_1$
$t_2=15+2x_2$
and total flows from 1 to 2.
$q_{12}=12$
Substituting the travel time in formulation of system optimal, we get the following:
$min \colon \ Z(x) = x_1;\ 10 + 3x_1^2+x_2(15+2x_2)$
$10x_1+3x_1^2+15x_2+2x_2^2$
Substituting $x_2=12 - x_1$ in the above formulations take the following form:
$10x_1+3x_1^2+15(12-x_1)+2(12-x_1)^2$
Differentiate the above equation w.r.t $x_1$ and equate to zero, and solving for and then $x_2$ leads to the solution $x_i^*=5.3$, $x_2^*= 6.7$, and $Z(x^*)=327.55$.
Brass‘s Paradox
- User Equilibrium assum‘s that driver‘s minimize their own travel cost without considering the impact on the network. Thus there is no guarantee that system travel cost will become less.
- If the traffic is assigned as per SO, the system travel cost will not increase with the addition of a link.
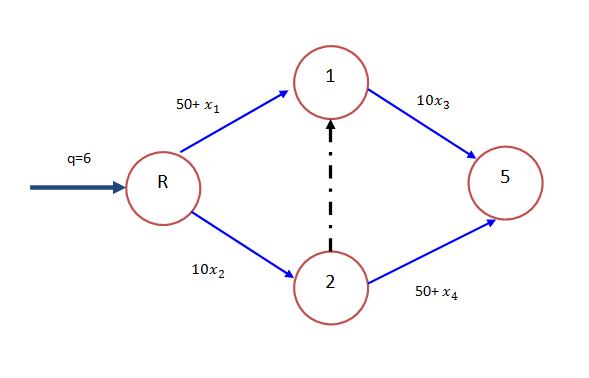
UE Formulation
$50+x_1+10x_3=50+x_4+10x_2$
$Path\ 1\ =\ R - 1 - 5$
$Path\ 2\ =\ R - 2 - 5$
Solving we get
$x1 = x2 = x3 = x4 = 3$
Cost for Path 1 = 83
Cost for Path 2 = 83
Thus System Cost = 498
Add additional link between nodes $1$ and $2$ with a hope to minimize the System Travel Cost.
Cost for Path 3 = 70 , Path 3 = R - 2 - 1 - 5
Since the travel cost obtained for one user for Path 3 is less than travel cost for Path 1 and Path 2 , some user's will shift to Path 3. Thus the new UE flow will be :
$50+x_1+10x_3=50+x_4+10x_2=10x_2+10+x_5+10x_3$
Solving we get $x_1 = 2$, $x_2 = 4$, $x_3 = 4$, $x_4 = 2$, $x_5 = 2$
Cost for Path 1 = 92, Path 2 = 92 and Path 3 = 92
Path cost increases with an introduction of extra link, similarly System cost also increases.
References Books
- J. De D. Ortuzar and L.G. Willumsen (1996), Modelling Transport. Wiley Publications, London.
- Y. Sheffi (1985), Urban Transportation Networks: Equilibrium Analysis with Mathematical Programming Methods. Prentice-Hall Inc., Englewood Cliffs, New Jersey.